Optimization Algorithms (2주차) 정리

*다음 내용은 Andrew ng의 Deep Learning Specialization 과정 중 일부 강좌를 정리한 강의 노트입니다.

틀린 내용이 있다면 말씀해주세요.

 

Mini-batch Gradient Descent

machine learning : 매우 empirical process이다. 즉 반복적인 작업이 많다. 따라서 빨리 모델을 훈련시키는 것이 중요하다.

→ 난점: 딥러닝은 big data일 때 더 잘 작동하는데 big data일수록 훈련하는 데에 있어 시간이 많이 소요된다.

 

Batch : 모델 학습 중 parameter를 업데이트할 때 사용할 데이터 개수

일반적인 Batch는 훈련예제 전부를 한번에 train하는 것이다. 그런데 m이 500만인 경우, 한번 훈련시키는데 시간이 많이 걸리므로 훈련 예제의 크기를 지정해서 조금씩 할 수도 있다. 위 이미지의 경우 batch size를 1000으로 정한 경우이다.

(위 이미지에서 {}로 표시한 것이 각 미니 배치를 나타낸 것이다.)

이를 이용해서 사용하는 gradient descent를 mini-batch gradient descent라고 한다.

그리고 이 경우에 mini batch의 개수는 5000개이다.

1000 크기의 미니 배치로 파라미터를 업데이트하는 과정을 1 epoch이라고 할 수 있다. 

이 경우 한번의 GD에서 5000 epoch를 진행한다. 따라서 또 하나의 for loop이 필요한 셈이다.

m이 매우 클 때, mini batch는 batch보다 훨씬 더 빠르게 진행된다고 한다.

 

Understanding Mini-batch Gradient Descent

그렇다면 Mini batch가 대규모의 데이터 세트에서 왜 더 효과적일까? 

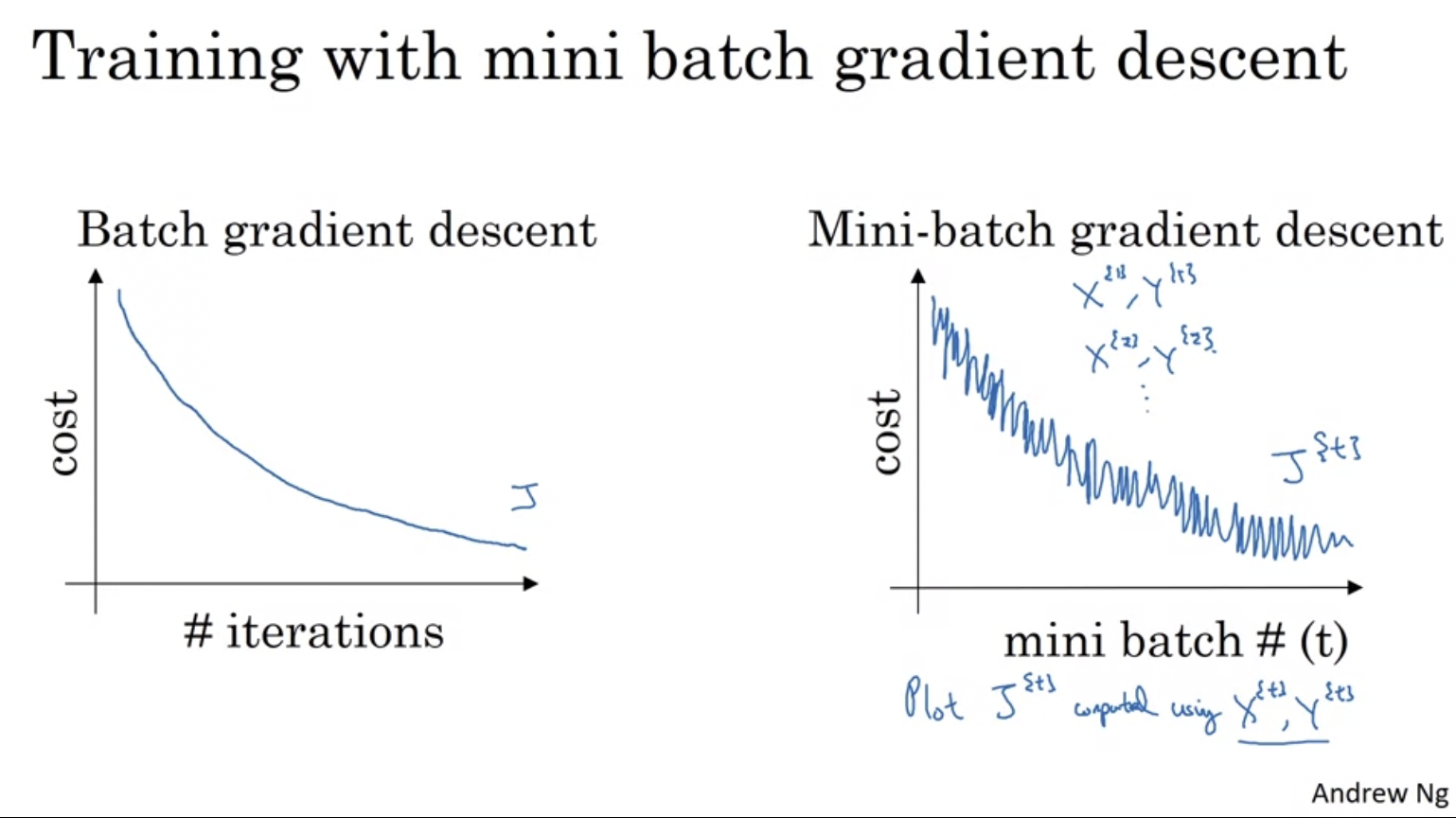
batch gradient descent (전체 트레이닝 세트를 돌리는 것)에서는 매 반복마다 cost가 무조건 감소할 것이다. 이에 반해 mini batch gradient descent에서는 매 반복마다 X{t}, Y{t}를 처리하는데 그러할 경우 noisy함이 발생할 수 있다.

 

골라야 하는 매개변수 (하이퍼 파라미터) : mini batch size

너무 작으면(1, Stochastic gradient descent) 수렴이 되지 않고 최소점 주위를 계속 맴돈다 : 속도를 잃는다. 

너무 크면 (m) : Batch graident descent와 유사하다. 한번 돌리는데 너무 오래걸린다. (Too long per iteration)

 

그 사이에 있는 어느 값(1 ~ m)이 두 가지의 장점이 있다. (속도도 높이면서, 기다릴 필요 없음) ㄷ

⇒ 그 사이 값을 가지려면?

1. small training set인 경우 (less than 2000) : 그냥 batch로 할 것. mini batch는 의미가 없다
2. m이 크다면, mini batchsms 64 ~ 512 정도가 보편적이다. 2의 지수일 때 더 빨리 실행되는 경향이 있다고 한다.

⇒ 주의할 점 : 모든 mini batch가 CPU, GPU에 있도록 한다. 몇 개 시도해보고 가장 효율적인 것 하나를 고르면 된다.

 

Exponentially Weighted Averages

여러 최적화 알고리즘을 이해하기 위해서는 exponentially weighted averages에 대해 알고 있어야 한다. 

Exponentially Weighted Averages (지수 가중 평균, EMA라고도 부른다) : 데이터의 이동 평균을 구할 때, 오랜 데이터가 미치는 영향을 지수적으로 감소하도록 만들어주는 방법

런던 날씨를 통해 개념을 이해해보자. 각 날짜별로 온도가 위와 같을 때, 다소 noisy함이 있고 우리는 이에 대한 Trend(전반적인 흐름)를 알고 싶다고 가정해보자. 즉 시간의 흐름에 따라 이 데이터가 어떻게 움직이는지 경향성을 알고 싶을 때 무엇을 할 수 있을까?

 

우리는 오래된 데이터와 최신 데이터에 대해 가중치를 붕여할 수 있다.

출처 : https://wooono.tistory.com/225

 

나중에 배우게 되겠지만, Vt는 1/1-베타 days 온도의 대략젹인 평균을 의미한다.

따라서 베타가 0.9인 경우 10일의 평균이며, 이는 빨간색으로 표시된다. 

베타가 0.98인 경우 50일의 평균이며, 이는 초록색으로 표시된다. (훨씬 완만한 곡선) 50일의 평균이다보니 온도 변화에 따라 즉각적으로 반응하지않고 느리게 값이 변한다. 

베타가 0.5인 경우 2일의 평균이며, 노란색으로 표시된다. 이는 빠른 온도변화를 즉각적으로 반응하게 될 것이다.

 

(나의 추측) 베타가 크면 클 수록 과거의 영향력에 대해 더 많은 가중치를 부여하게 된다. 그래서 더 이전 일들의 날들까지 고려할 수 있는 것, 반면 베타는 지수적으로 곱해지기 때문에 (예를 들어 Vt는 Vt-2의 베타 제곱이 부여됨.) 베타가 줄면 줄수록 빠르게 이전 날들의 영향력이 사라지게 될 것이다. 

 

다음 영상에서 이에 대한 직관을 더 살펴보자.

 

Understanding Exponentially Weighted Averages

v100을 생각해보자. 0.1 v99 + 0.1 theta100은

0.1 * (0.9 v98 + 0.1theta99) + 0.1 theta 100 으로 표현할 수 있다. 그리고 끝도없이 내려갈 수 있다.

 

따라서 이것을 식으로 표현하면, x축이 theta일 때 이전으로 갈 수록 점점 지수형태로 내려갈 것이다.

 

 

저번에 얘기한 공식이 나온 과정

0.9^10하면 얼추 값이 0.35가 되고, 이 값은 대략 1/e이다. 즉, 지수그래프가 3분의 1 정도로 감소하는 데에 10일 정도가 소요되고, V가 0.9인 경우 직전 10일의 기온을 집중하여 지수 가중 평균을 구하는 것과 같다고 한다. 일반적으로 아래 그림처럼

이렇게 표현한다고 한다.

그러면 이게 실제로 어떻게 구현되는가?  

 

큰 장점 : 효율성

계속해서 하나의 Vtheta에 값을 갱신하며 저장하면 되므로, 많은 메모리가 필요하지 않다.

또한 코드로 보았을 때 한줄이면 구현되므로, 머신 러닝에서 사용할 수 있다.

→ 물론 정확한 평균 계산법은 아니다. 하지만 정확한 평균을 구하기 위해서는 그동안의 기온을 모두 보관하고 더해야하기때문에 더 많은 메모리가 필요하다.

다음 영상에서 이를 활용한 몇가지 예제를 살펴볼 예정

 

Bias Correction in Exponentially Weighted Averages

bias correction : EMA에서 더 정확하게 평균을 구할 수 있도록 하는 technical detail

 

실제 위 식을 이용하여 EMA를 구하면,

초록색 곡선보다는 보라색 곡선이 나온다. 보라색 곡선은 보면 알다시피 초반 곡선이 매우 낮다.

 

why? : V0이 0으로 초기화되면, V1에서 0.98 * 0 + 0.02 * theta1인데, 앞 0.98이 사라져버리므로 그냥 현재 data에 0.02 값을 곱한 것이 된다.  V1이 낮게 설정되면 그 이후 값들도 한동안 계속 낮은 값을 유지하게 된다. (이전 값의 beta 제곱이기 때문이다.)

 

여기서 t : 현재 요일

 

Bias Correction : Vt 대신 vt / 1- beta^t를 사용하는 것이다. t값이 커지면 beta^t는 0으로 수렴하게 된다. 값이 작으면 Vt에 큰 값이 부여된다. 이런 식으로 함으로써 초반 그래프에 대한 bias를 어느정도 해소할 수 있다. 

 

이를 통해 보라색 그래프가 초록색 그래프로 맞춰 들어가게 된다.

→ 보통 사람들은 Bias Correction을 신경쓰지않는다고 한다. (initial phase에 한정되기 때문이다)

Gradient Descent with Momentum

momentum(관성) algorithm : 변수가 가던 방향으로 계속 가도록 속도를 추가해준다.

일반적으로 GD보다 항상 더 빨리 작동한다.

기본적인 아이디어 : gradient의 EMA를 구하는 것

 

일반적인 GD

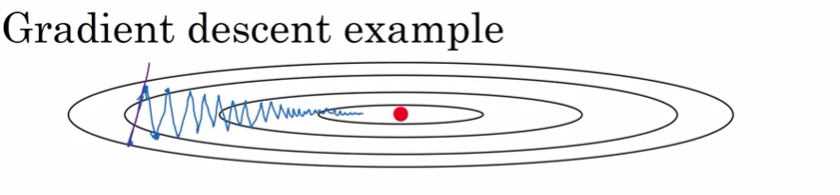
위와같이 변동폭을 거치며 최소점으로 나아간다.

 

더 큰 learning rate를 사용하는 경우, 오버슈팅이 발생할 수 있다. 따라서 작은 learning rate를 사용해야 한다.

 

따라서 위 그림에서 세로축의 경우에는 느리게 학습하길 원할 것이다.

그런데 이와 반대로 가로축에 대해서는 더 빠르게 학습하길 원할 것이다.

 

모멘텀을 사용하면, 다음과 같이 작동하게 된다.

 

이 과정은 앞서 구했던 EMA 과정과 유사하다. (momentum 개념의 통계학적 관점) 현재 batch에서의 dw,db를 구하고, 이에 대해 EMA를 구한다. 이를 통해 w, b를 업데이트 한다. 이 과정을 통해 GD의 noise를 낮추고 조금 더 완만하게 만들 수 있다. 세로축의 변동은 거의 0이 되고, 가로축의 변동은 꽤 큰 값이 되어서, 빨간색 직선과 같은 현상이 나온다.

 

또 하나의 직관으로, 공이 굴러가는 모습을 생각해볼 수 있다. (momentum 개념의 물리학적 관점)

여기서 dw, db는 가속을 의미하고, Vdw, Vdb는 속도를 의미한다고 할 수 있다.

그런데 여기서 beta가 0에서 1 사이이므로 적절한 마찰력을 준다.(friction)

 

여기서 하이퍼파라미터 : alpha, beta 보통 bata는 0.9로 둔다고 한다. (지난 10번의 GD 평균치라고 할 수 있다)

 

bias correction을 적용할 수도 있지만, 실제로는 잘 안쓴다. 초반 몇 번 이후로는 적용할 필요가 없기 때문이다.

 

논문에서는 위 그림에서 오른쪽 부분과 같이, (1-beta)가 생략되어있는 경우도 있다. 실제로 작동하는 것은 비슷하게 작동할 수 있지만, 덜 직관적으로 보여 ng은 왼쪽과 같은 공식을 더 선호한다고 한다. 

WHY? : Vdw, Vdb가 바뀌면서 learning rate인 alpha도 retune(재조정)해야 하기 때문이다. 

 

단순히 dw를 빼는 GD보다 이렇게 momentum을 적용한 방식이 훨씬 빠르게 동작한다.

 

RMSprop

RMSprop : Root Mean Square prop

gradient descent 속도를 높일 수 있는 또 다른 알고리즘이다. 

 

수평의 변화를 w, 수직의 변화를 b로 가정해보자. 우리는 수평의 변화는 유지하면서 수직의 변화를 줄여, learning rate를 키워도 오버피팅이 발생하지않도록 하고싶을 것이다.

 

기존 변화량을 보면, 위 이미지처럼 수평의 변화보다 수직의 변화가 훨씬 큰 편이다.

 

위 그림처럼 b가 세로축이고 w가 가로축일 때, dw^2 보다도 db^2가 훨씬 더 클 것이다. (여기서 제곱은 각 요소별 제곱이다)

따라서 이 값을 dw, db에 나누어주면 더 큰 값이였던 b는 감소하고, 작은 값이었던 w는 거의 감소하지 않을 것이다.

이러한 방식으로 기울기를 낮추어 학습 속도를 더 높일 수 있다.

 

Root Mean Square prop이라는 이름 그대로, EMA 제곱 평균을 구하고, 이를 루트 씌어서 나누는 것이다.

 

물론 실전에서는 dw, db는 단순 2차원이 아니라 다차원이기 때문에 이렇게 여러 가중치의 합이 하나의 축을 나타내기 될 것이다. 

 

그래서 위에서 말한 가로축/세로축을 분리한 것은 그냥 설명을 위해 나타낸 것이라고 보면 된다. 

 

Sdw, Sdb가 0이 되면, 0을 나누게 되면서 값이 폭발적으로 증가하게 될 것이다. 이를 방지하기 위해 매우 작은 값의 엡실론을 분모에 추가한다. 보통 10^-8을 곱한다고 한다. momentum과 RMSprop 모두, 더 큰 learning rate를 사용할 수 있도록 기울기가 무뎌지고, 이를 통해 알고리즘 학슴률을 높일 수 있다.

 

재밌는 사실 .. : RMSprop은 학술 논문에서 처음 나온 것이 아닌, 몇년전에 Jeff Hinton이 coursera강의에서 처음 제안했다고 한다.

 

다음 영상에서, momentum과 RMSprop를 합친 알고리즘에 대해 배울 것이다.

 

Adam Optimization Algorithm

 

2주차에서 배운 것들을 다 때려박은 느낌이다.

1. 현재 batch에서 dw, db를 계산 (만약, 제일 단순한 GD였으면 현재 w, b에서 각각 dw, db를 빼는 식으로 업데이트 끝)
2. 모멘텀을 적용하여 Vdw, Vdb를 구함
3. RMSprop를 적용하여 Sdw, Sdb를 구함 (베타의 혼동을 방지하기 위해 1, 2 표시해줌)
4. Adam 알고리즘에서는 bias correction과정도 거침. 그래서 각 Vdw, Vdb, Sdb, Sdw에 대해서 적용시켜줌. (1-beta^t를 나눠주어 초반에 값이 극도로 낮음을 보정해준다)
5. 업데이트틑 수행해준다. 업데이트를 하는 모습을 보면 momentum과 rmsprop를 합쳐서 사용하고 있음을 알 수 있다. (Vdw는 momentum의 방식으로, Sdw는 rmsprop의 방식으로)

momentum에서 사용하는 하이퍼 파라미터는 beta1, rmsprop에서 사용하는 하이퍼 파라미터는 beta2이다. 

Adam에서 사용한 하이퍼파라미터들에 대해 알아보자

 

알파(learning rate) : 중요한 파라미터이며 하이퍼파라미터 튜닝을 할 필요가 있어보인다. 여러 값들을 넣어보며 test해봐야한다.

 

beta1은 전에도 말했다시피 0.9를 default값으로 사용. beta2는 0.999를 사용할 것을 Adam이 추천함.

엡실론은 그리 중요한 하이퍼파라미터는 아님. 보통 10^-8로 설정

 

Adam = adaptive moment estimation

 

Learning Rate Decay

하이퍼파라미터인 learning rate를 설정하는 것과 관련해서 알아보자. 

 

Learning Rate Decay : 시간이 지남에 따라 learning rate를 서서히 줄이는 것이 속도를 높이는 데에 도움이 된다. 

 

왜일까?

 

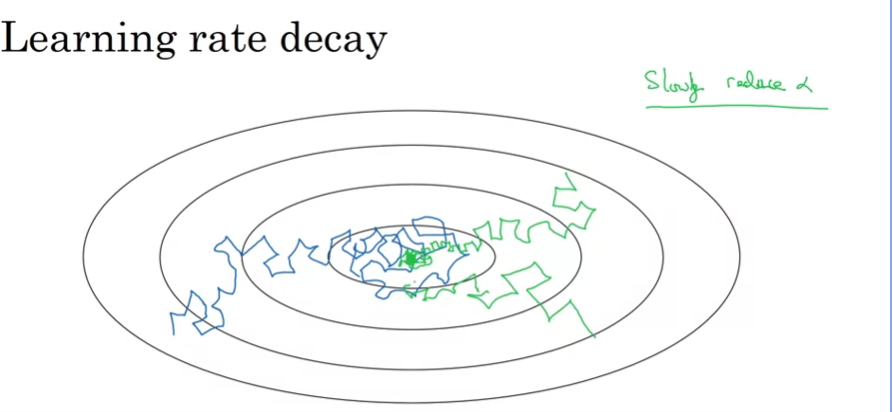
직관적인 설명 : Learning rate를 항상 크게 유지하면, 남색 선을 보아도 알 수 있듯이, mini batch는 noisy함이 있으므로 계속 주위를 크게 배회하게 될 것이다. 이와 반해 학습률을 점점 줄여나가면 똑같이 배회해도 좁은 범위 안에서 진동할 것이다. 우리가 처음에 학습할 때는 크게크게 가도 좋지만, 점점 최저점에 가까워질 수록 줄이는 것이 직관적으로 보았을 때에도 더 좋을 것이다.

 

어떻게 구현하는지 살펴보자.

learning rate decay 공식은 다음과 같다.

여기서 decayrate는 또다른 하이퍼파라미터로 볼 수 있을 것이다. 

 

 

learning rate decay 방법은 다양하게 있다. 지수배로 갑소하는 것이 있고, 단계별로 감소하는 것이 있다. 이렇게 공식을 이용할 수도 있지만 직접 수작업을 하는 경우도 있겠다. 일단 모델을 돌려보고 적절히 줄일만한 지점을 찾아보는 것이다. 소수에 모델에 대해서만 적용가능하겠지만, 그렇게 하는 사람들도 있다.

 

The Problem of Local Optima

딥러닝 초기에 local optima에 대한 많은 걱정이 있었다. 하지만 딥러닝이 발전하면서 그 문제에 대한 이해 또한 변하고 있다.

그 문제가 무엇인지, 최근에는 이 문제에 대해 어떻게 보고 있는지 알아보자.

원래 걱정했던 현상 : global optima(우리가 원하는 최저점)에 도달하기 전에, 여러 local optima에 빠지게 될 까봐

 

하지만 이러한 직관은 옳다고 볼 수 없다. 실제로 신경망을 만들게 되면 굉장히 고차원적이어서 cost function에서 위와 같은 local optima가 나올 확률이 굉장히 낮아진다.

 

기울기가 0인 지점은 이렇게 아래로 볼록하거나 위로 볼록한 경우인데, 20000차원이 있을 경우 모든 차원이 아래로 볼록한 형태를 띄어야 한다. 하지만 그럴 확률은 매우 낮다.

오히려 실제 신경망을 만들면 local optima보다는 saddle point(안장점)를 만날 확률이 높다. 아래로 볼록한 지점과 위로 볼록한 지점이 겹치는 경우인데, 마치 말의 안장같아서 그러한 이름이 붙여진 것 같다.

 

 

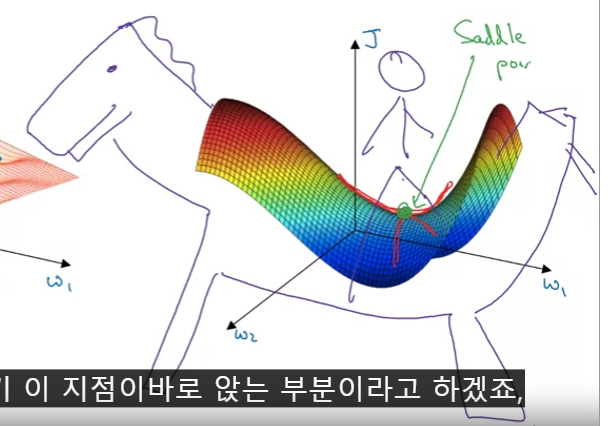
실제 딥러닝에서 local optima를 만날 확률이 없다면, 어떠한 점이 문제가 될 수 있을까.

아래와 같은 plateaus에서 학습 속도가 느려질 수 있다.

plateaus는 미분이 오랫동안 0에 가까운 영역을 의미한다.

 

알아둬야할 사실

1. 굉장히 고차원의 신경망에서는 local optima에 빠질 확률은 낮다.
2. 그러나 plateaus에 빠질 수는 있는데, 이러한 경우 Adam, momentum, RMSprop이 도움이 될 수 있다.