Hyperparameter Tuning, Batch Normalication and Programming Frameworks (3주차) 정리

Tuning Process

Hyperparameter을 세팅하는 법. 즉 체계적으로 최적의 Hyperparameter를 찾아내는 법에 대해 알아보자.

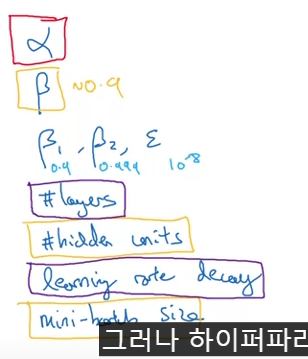
빨간색으로 표시한 alpha, 즉 learning rate이 제일 중요하다.

그 다음에는 노란색으로 표시한 모멘텀 알고리즘에서 사용하는 beta, mini batch size, hidden unit의 개수정도가 중요하다.

그리고 세번째로 중요한건 보라색으로 표시한 layer의 개수, learning rate decay가 중요할 것이다. 그 외에는 Adam 알고리즘에서 사용하는 것들인데, 이것들은 사실상 값이 고정되어있어서 큰 의미는 없다. (물론 정해진 답이 있는 문제는 아니다.)

 

그렇다면, 튜닝할 값의 집합을 어떻게 선택할까?

 

하이퍼 파라미터의 개수가 많지 않을 때에는, 왼쪽처럼 그리드(격자판) 구조로 찾아가면서 가장 잘 작동하는 값들을 찾곤 했다. 그러나 딥러닝에서는, 오른쪽 이미지처럼 임의 선택하는 것이 더 낫다. 왜냐하면 어떤 하이퍼파라미터가 중요할지 미리 알기 어렵기때문이다.

 

예를 들어 hyper1은 learning rate이고, hyper2는 epsilon이라고 해보자. learning rate이 압도적으로 영향을 끼치므로, 왼쪽 그리드 구조에서는 25개의 값을 시도해봤지만 실질적으로 5개의 알파값만 시도해볼 수 있었다. 이에 반해, 오른쪽 구조에서는 임의로 선택하기 때문에 25개의 알파값을 시도해볼 수 있을 것이다. 즉 이렇게 하이퍼 파라미터의 중요도가 다른 상황에서는 그리드 구조가 오히려 비효율적일 수 있다. 

 

또한, Coarse to fine 탐색도 자주 이용되는 방식이다.

coarse하게 탐색하다가, 파란색 사각형 내부에서 더 잘 동작함을 확인하면,

그 범위 내에서 밀도를 높여서 다시 탐색해보는 방법을 의미한다.

 

tuning에 있어서 다음 두 가지 기술이 있다. 

 

1. 랜덤 샘플링
2. (선택) course to fine

어떠한 규모에서 하이퍼파라미터를 선택할지에 대해 다음 영상에서 설명하겠다.

 

Using an Appropriate Scale to pick Hyperparameters

sampling at random이 sampling uniformly at random을 의미하지는 않는다.

 

랜덤으로 하이퍼파라미터를 선택하는 데에 있어, 적절한 범위를 선택하는 것이 중요할 것이다. 예를 들어 위 hiddn unit의 개수는 50에서 100개 사이일 때 잘 동작하고, layer의 개수는 2개에서 4개 사이일 때 잘 동작한다고 가정해보자.

 

learning rate를 결정한다고 해보자. 경계선이 0.0001 ~ 1이라고 해보자. 균일하게 샘플링을 진행하는 것(linear scale)보다는 log 스케일로 샘플링을 진행하는 것이 더 합리적이다.

 

로그 스케일로 샘플링을 진행하는 방법에 대해 알아보자.

10의 지수를 활용하자.

일반적으로 10^a, 10^b 범위로 할 경우, 10^a = 0.001이고, 로그 10을 취하면 a = -4임을 알 수 있다. 같은 방법으로 b가 0인 것도 알 수 있다. 따라서 r은 -4에서 0 사이이다.

 

이제 EMA에서 beta를 구하는 방법에 대해 살펴보자 .

 

beta가 0.9에서 0.09 사이 범위를 가진다고 해보자.

1-beta는 0.1에서 0.001이다. 이전 방식을 이용하면 -1에서 -3이다. (이전과는 반대로 더 큰 값이 왼쪽에 있다. 그리고 1-beta = 10^r이므로 beta는 1 - 10^r이다.

왜 선형적으로 탐색하는게 좋은 방법이 아닐까? 어디 위치하느냐에 따라 값의 변화가 주는 영향이 다르기 때문이다. 만약 beta가 0.9에서 0.9005(10개 예제가 늘어난 평균)로 변하는 것은 큰 영향을 주지 않겠지만, 0.99에서 0.9905(1000개 예제가 늘어닌 퍙군) 로 바뀌는 것은 매우 큰 변화가 있을 것이다. 따라서 beta가 1에 가까울 때 작은 변화에 매우 민감해진다. (??)

 

Hyperparameters Tuning in Practice: Pandas vs. Caviar

 

딥러닝은 많은 분야에 응용되고 있으며, 한 분야에서 사용되는 아이디어는 다른 분야에도 적용해볼 수 있다. 따라서 딥러닝 개발은 다른 영역의 논문을 많이 읽고 영감을 얻는 것도 유용하다.

이와 마찬가지로 하이퍼 파라미터도 시간이 지나면 더 최적의 방법이 나올 수 있고, 혹은 데이터 셋의 변경이 있을 수 있다. 따라서 주기적으로 하이퍼파라미터 테스트를 하며 재평가의 과정을 거치는 것이 중요하다.

다음으로 하이퍼 파라미터를 탐색하는 두 가지 방법에 대해 알아보자.

 

연산을 위한 Resource가 많지 않아 한번에 한 모델만 훈련시킬 수 있을 때 사용된다. 한가지 모델에 대해 짧게는 몇일 길게는 몇주동안, 매번 다르게 하이퍼파라미터(학습률)를 조정해가며 학습해나가는 것이다. 그러다가 학습률이 너무 높아지면, 다시 이전으로 돌아가는 식으로 진행된다. 이렇게 인내심있게 지켜보며 거기에 맞게 학습률을 계속 조정해주는 것을 Babysitting one model이라고 한다.

 

또 다른 방법은 병렬식으로 여러 모델을 동시에 훈련시키는 방법이다.

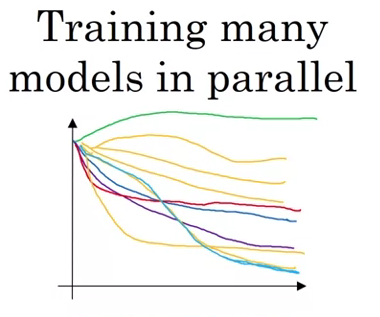
여러 모델을 병렬적으로 돌릴 수 있으면, 각기 다른 learning rate를 적용하여 학습을 동시에 진행하고, 더 잘 감소하는 형태의 learning rate를 고를 수 있다.

이 두 가지 방법 중 선택 기준은 얼마나 conputational resource를 가지고 있느냐에 따라 달라진다.

가능하면 후자가 좋겠지만, 컴퓨터 비전 영역같이 데이터가 무수히 많아서 여러 모델을 동시에 돌리지 못하는 경우, 전자의 방식도 많이 한다.

 

Normalizing Activations in a Network

Batch normalization : 딥러닝에서 가장 중요한 아이디어 중 하나

BN을 통해 하이퍼파라미터 search 문제가 훨씬 쉬워지고, 신경망을 더욱 강하게(robust, 민감하지 않게) 만들어주었다.

 

BN이 어떻게 동작하는지 알아보자.

 

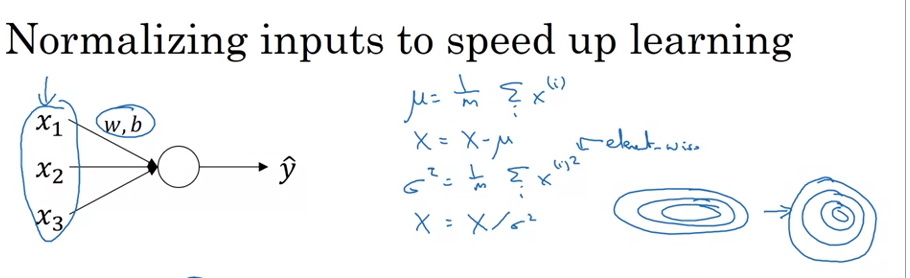
앞서 우리는 linear regression, logistic regression에서 입력의 정규화가 학습 속도를 높일 수 있음을 배웠다. (위 이미지에서 분산을 나누는 거로 잘못 표시되어있는데, 표준편차(루트분산)를 나누는 것이다!!)

 

그렇다면, DNN에서는 어떨까?

 

w[3], b[3]을 기준으로 했을 때, 입력은 a[2]이고, 이를 정규화할 수 있을 지 알아보자.

 

활성화함수와 Batch norm중 어떤 것을 먼저 적용할지에 대해서는 여러 논쟁이 있는데,

일단 default로는 z[2]에 대해서 batch norm을 적용한 다음에 활성화함수를 적용하는 것을 추천한다고 한다.

Batch norm을 어떻게 구현하는지 알아보자.

 

l번째 레이어에 W(l) + b(l)의 결과인 z[l]이 z(i) .. z(m)까지 있다고 가정해보자. 그럴 때 이 값들에 대한 평균과 분산을 구하여 정규화를 진행한다. 그러면 평균은 0, 분산은 1로 이루어질 것이다.

 

하지만 모든 hidden unit의 평균이 0이고 분산이 1이 되기는 원하지 않을 것이다. 따라서 마지막에 learnable parameters인 gamma와 beta를 통해서 원하는 값이 만들어지도록 할 것이다. z(i)들의 평균과 분산에서 일부는 다른 분포도를 가지도록 하는 것이다. 

 

다음영상에서 이러한 batch norm을 신경망에 맞추는 방법에 대해 알아볼 것이다.

아직은 BN이 무슨 도움이 되는건지 안와닿을 수 있는데, 이후 영상을 통해 알 수 있게 될 것이다.

 

Fitting Batch Norm into a Neural Network

 

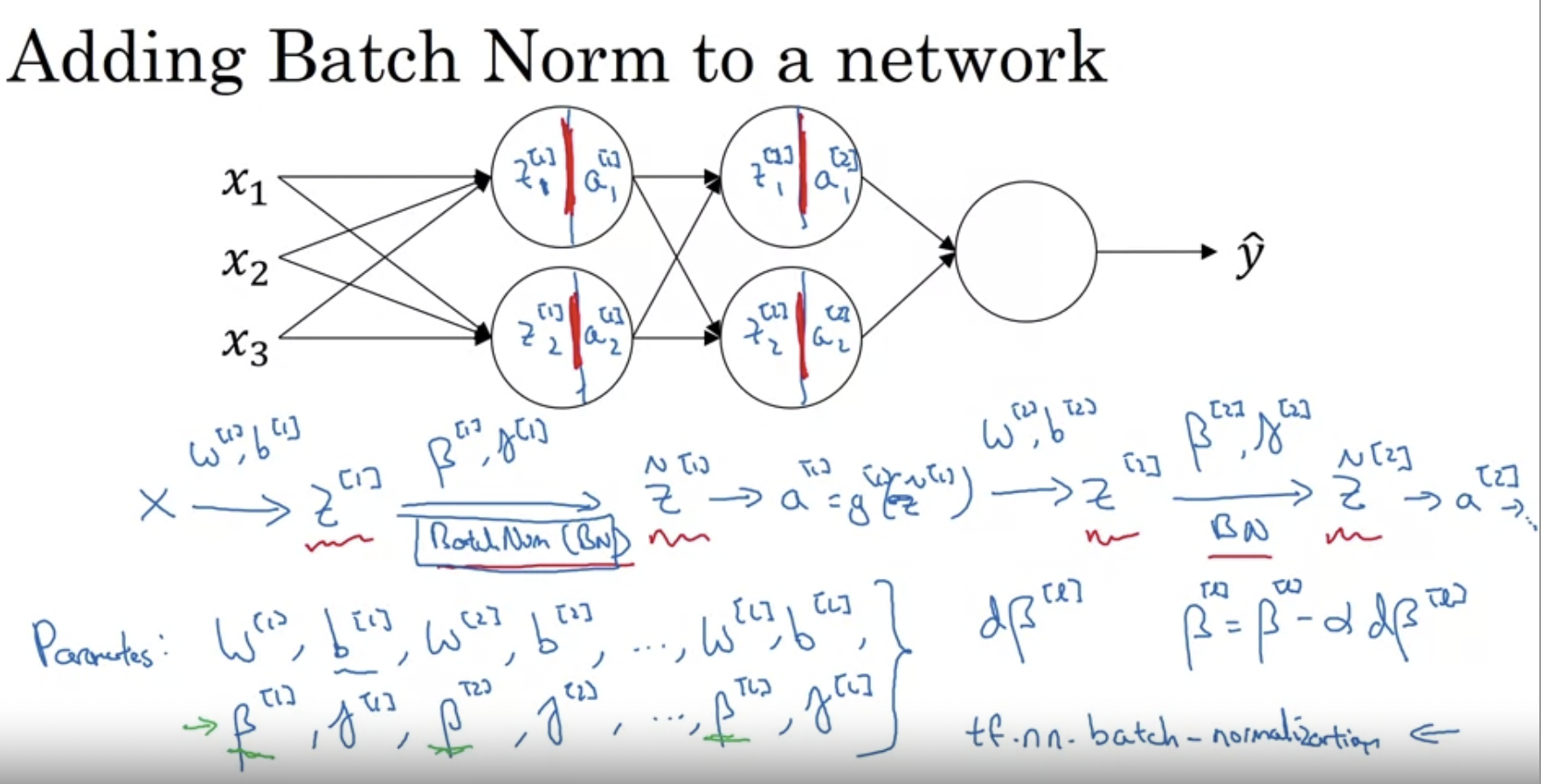
신경망 안에서 Batch Norm이 구체적으로 어떻게 작동하는지를 살펴보자. 

Batch Norm은 원래 계산 과정에서 Z와 a 사이에 적용된다. 즉 각 layer에서 z[l]을 계산하면, 활성화함수가 적용되기 전에 BatchNorm을 진행한다. 그리고 역전파에서 w, b뿐만 아니라 beta, gamma(어느정도로 normalization할건지 결정하는 파라미터) 도 업데이트를 진행하며 훈련한다. 참고로 여기서 beta는 Adam, momentum 최적화에서 beta와는 별개의 것이다.

 

이러한 진행과정을 갖고 있지만, 실제로 텐서플로우같은 framework를 이용한다면, 오른쪽 아래 처럼 한줄로도 구현할 수 있다. 이러한 진행과정을 거친다는 점만 알아두자.

 

mini batch에서 batch norm을 적용하면 위와 같다. 여기서 주목할 점은, batch norm을 적용한다면 상수항이 큰 의미가 없다는 것이다. 어차피 input에서 평균값을 빼기 때문이다. 따라서 b 파라미터는 0으로 만들거나 무시할 수가 있다. 이 대신 beta[l]를 걸어주는데, 이것은 shift나 bias에 영향을 준다.

차원에 대해서도 알아둘 필요가 있는데, beta[l], gamma[l] 모두 b[l]과 동일하게 (n[l](hidden unit의 수), 1)이다.

 

지금까지 배운 내용을 종합하여, BN을 mini batch에서 구현하는 방식은 위와 같다. b에 대해서 back prop, update는 안해주어도 된다.

 

위는 GD를 이용한 것인데, 이것 말고 이전에서 배운 Adam, momentum, RMSprop를 적용할 수도 있을 것이다.

 

Why does Batch Norm work?

BN이 사용하는 이유 중 하나는 X 뿐만아니라 모든 hidden unit에서 정규화를 수행함으로써 학습률을 높여주는 것이다. 이번 영상에서는 이러한 직관에 대해 살펴보겠다.

 

logistic regrssion으로 구현한 유명한 고양이 분류 문제에서, 데이터 셋이 검은색 고양이에 대한 것이었는데 색깔 고양이에 대해 테스트를 한다고 하자. 그러면 잘 작동하지 않으며, 다시 훈련을 진행해야할 수 있다. 이러한 것을 Covariate shift (공변량 변화)라고 한다. 쉽게 말해데이터의 분포가 달라지면 모델이 제대로 작동하지 못하는 현상을 말한다. 

 

https://ko.d2l.ai/chapter_deep-learning-basics/environment.html

3.16. 환경 — Dive into Deep Learning documentation

 

 

 

 

이에 대해 뉴럴 네트워크에서는 어떠할지 보자.

 

 

layer 3을 기준으로 해보자.

입력으로 들어오는 a[2]1 .. a[2]4는 이전 w, b값에 영향을 받는다. 이 말은, 앞선 w, b가 변경되면 a값도 변경이 된다는 것이다. 따라서 a값은 고정된 것이 아니라 계속 변하게 되므로, covariate shift 문제가 발생할 수 있다. 이 변하는 값을 BN을 통해 줄일 수가 있다. 계속 값이 변경되더라도 평균값과 분산값을 내가 의도한대로 조절할 수 있기 때문이다.

 

뒤 레이어 입장에서는 이전 레이어들의 이동 폭이 크지 않으므로 (평균값과 분산값을 제어하므로) 더 학습을 쉽게 해준다.

즉, BN은 input값이 변하면서 생기는 문제들을 줄여준다. 따라서 다음 layer에서도 더 안정적으로 학습을 진행할 수 있다.

 

BN은 (약간의) regularization 효과도 있다.

사실 의도하지 않았고 미미한 효과라, 굳이 regularization의 목적으로 쓰지는 말라고 한다. mini batch의 평균과 분산을 이용하는 것이기 때문에, noisy함을 더해줘서 drop out과 같은 regularization 효과가 있다고 한다. 흥미로운 점은, mini batch의 크기를 늘리면 noisy함이 줄어서 해당 효과가 적어진다고 한다.

 

Batch Norm at Test Time

BN은 mini batch별로 실행하지만, test할 때는 mini batch가 아닌, 하나의 example에서 진행할 수도 있다.

따라서 이러한 경우 네트워크에 적용하는 방법에 대해 알아보자.

 

우리가 mini batch에서 적용하는 방식은 왼쪽과 같다. 하지만 test time에서는 mini batch만큼의 example이 없을 수도 있다. 따라서 평균과 분산을 구하는 별도의 방법이 필요할 것이다.

 

test set에서는 training set에서 구한 mini batch의 mu(평균)와 sigma(분산)을 활용한다. 실제로 사용할 때는 이를 활용해서 EMA를 사용하는 편이다. 직접 구하는 것과 비슷한 결과가 나오며, 프레임워크를 이용한다면 크게 걱정할 필요는 없다.

 

Softmax Regression

 

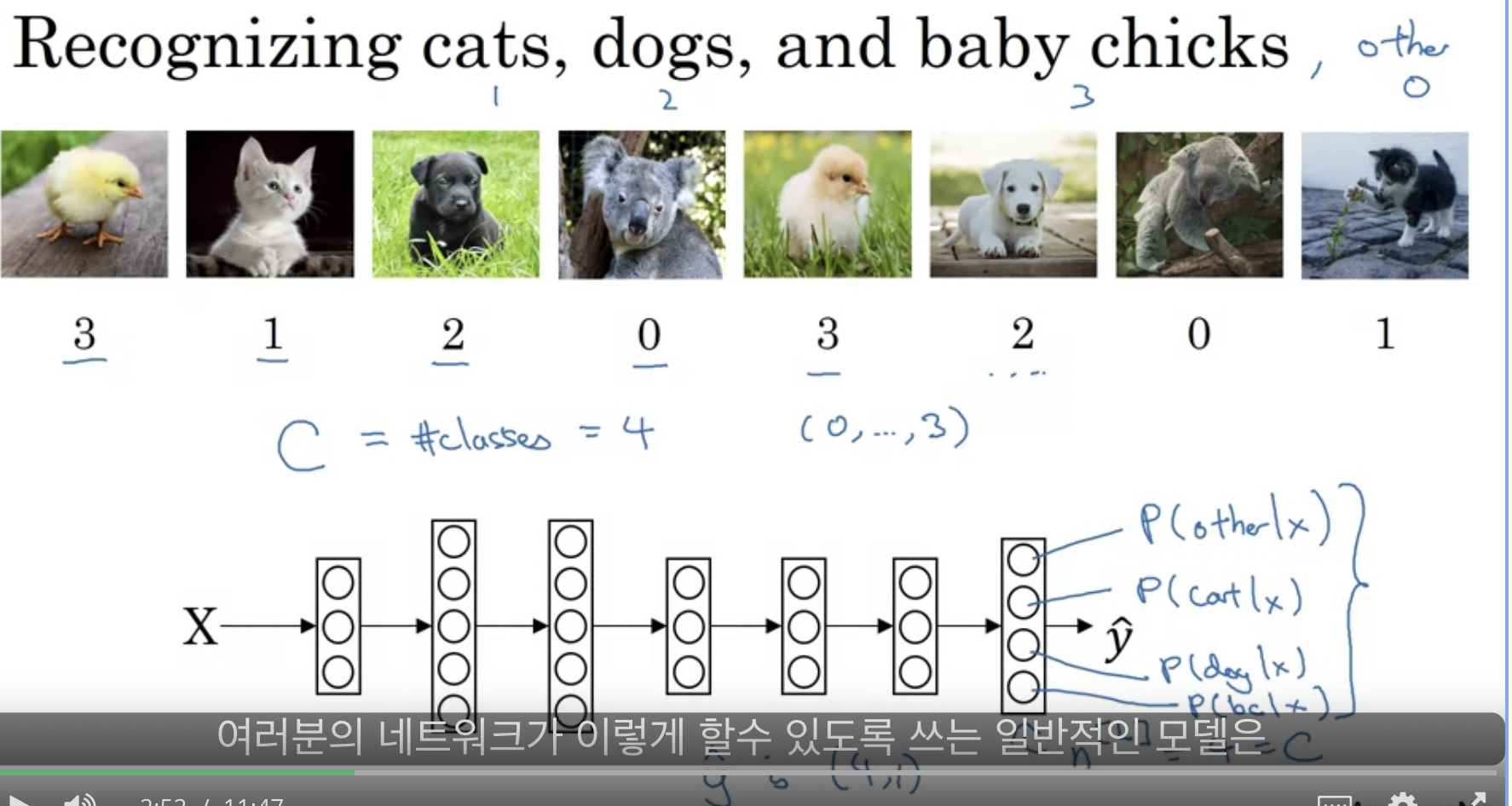
softmax regression : logistic regression의 일반화 버전

 

0, 1 이진 classification이 아니라, 다양한 클래스에 대한 예측을 하고 싶을 때 쓰는 모델이다. 출력으로 각 분류에 대한 확률을 낼 수 있는데, 이 확률의 합이 1이 되어야 할 것이다.

 

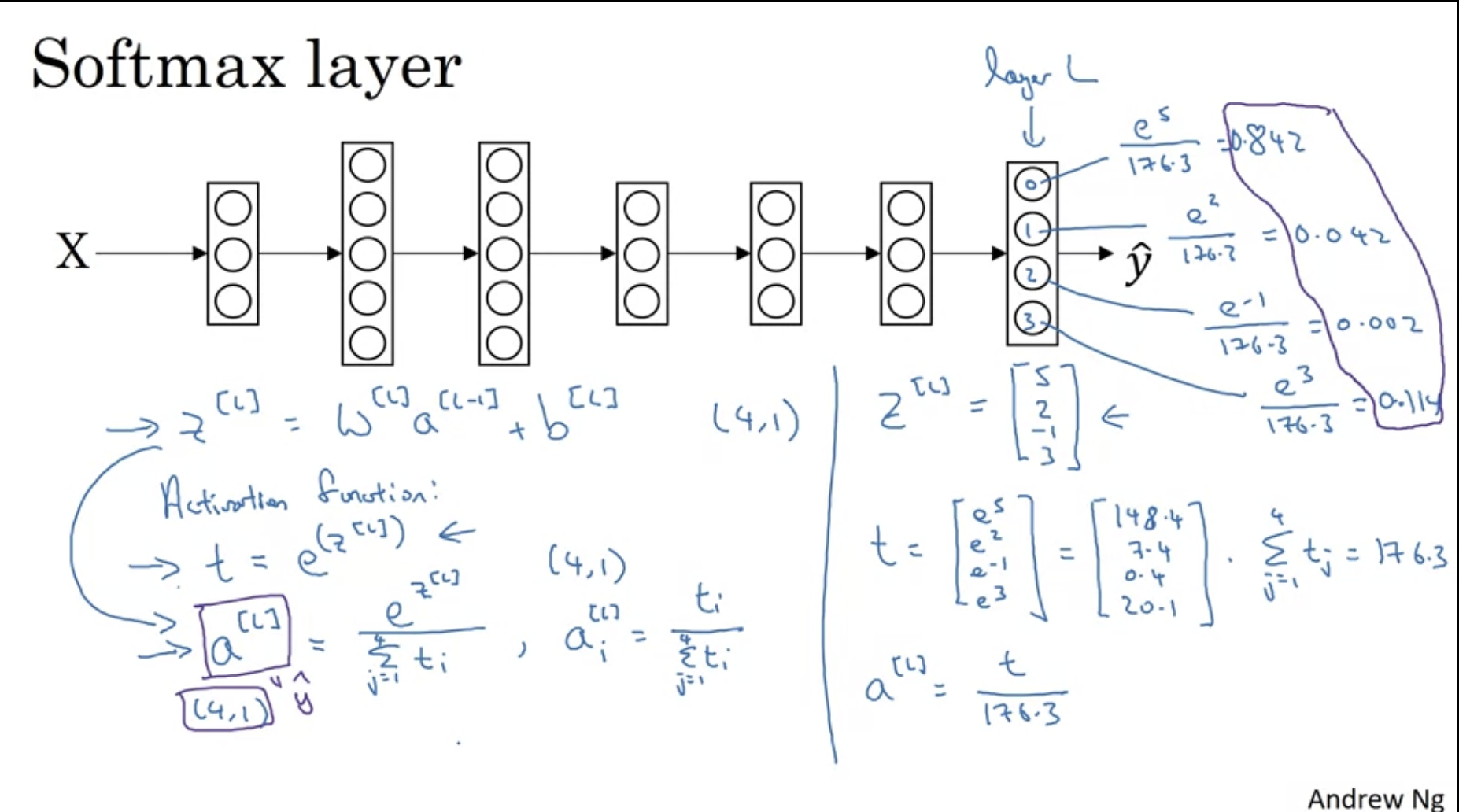
softmax 활성화함수를 적용하면, 그림에서 본 것과 같이, 들어온 벡터를 e의 지수로 올려주고, 전체를 더한 다음에 거기서 차지하는 비율을 반환한다.

 

그러면 모든 벡터의 합이 1이 된다. softmax의 독특한 점은, 벡터를 입력으로 받아서 벡터를 출력한다는 것이다. 예를 들어, 지금까지 다룬 sigmoid나 relu 활성화 함수를 보면, input과 output 모두 real number이다. 

 

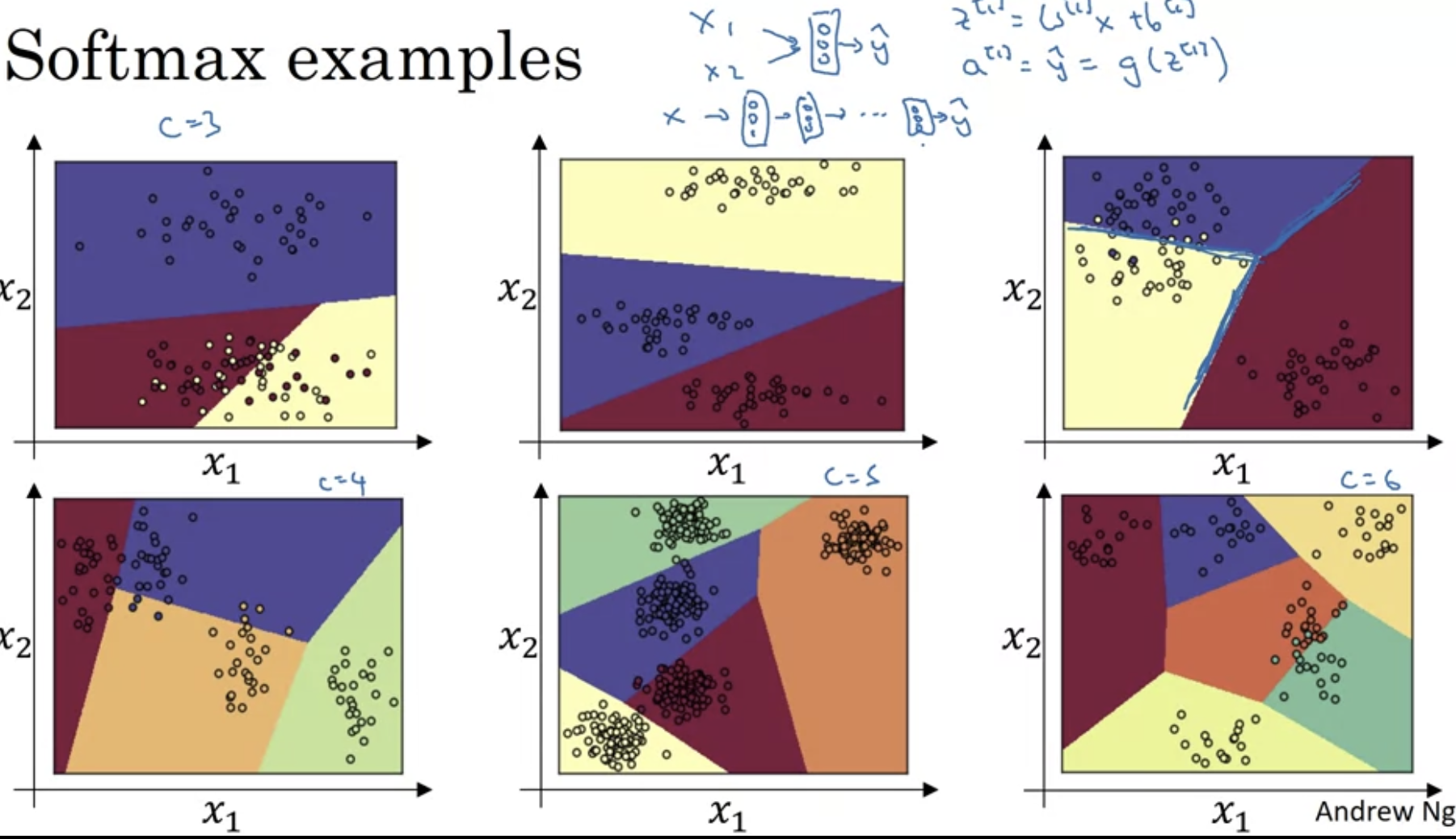
hidden unit이 없는 Linear regression에서, softmax는 이렇게 다양한 클래스의 분류를 수행할 수 있다.

 

Training a Softmax Classifier

softmax는 hardmax의 대조되는 개념으로 등장하였다. 

z[l]을 최종 확률값으로 변환한다고 해보자. hardmax의 경우 가장 높은 확률의 값을 1로 하고 나머지는 0으로 만들어준다. 이에 반해 softmax는 z[l]을 조금 더 부드럽게 매핑한다. softmax는 2개 이상 클래스에 대한 logistic regresiion의 일반화임을 알아두자.

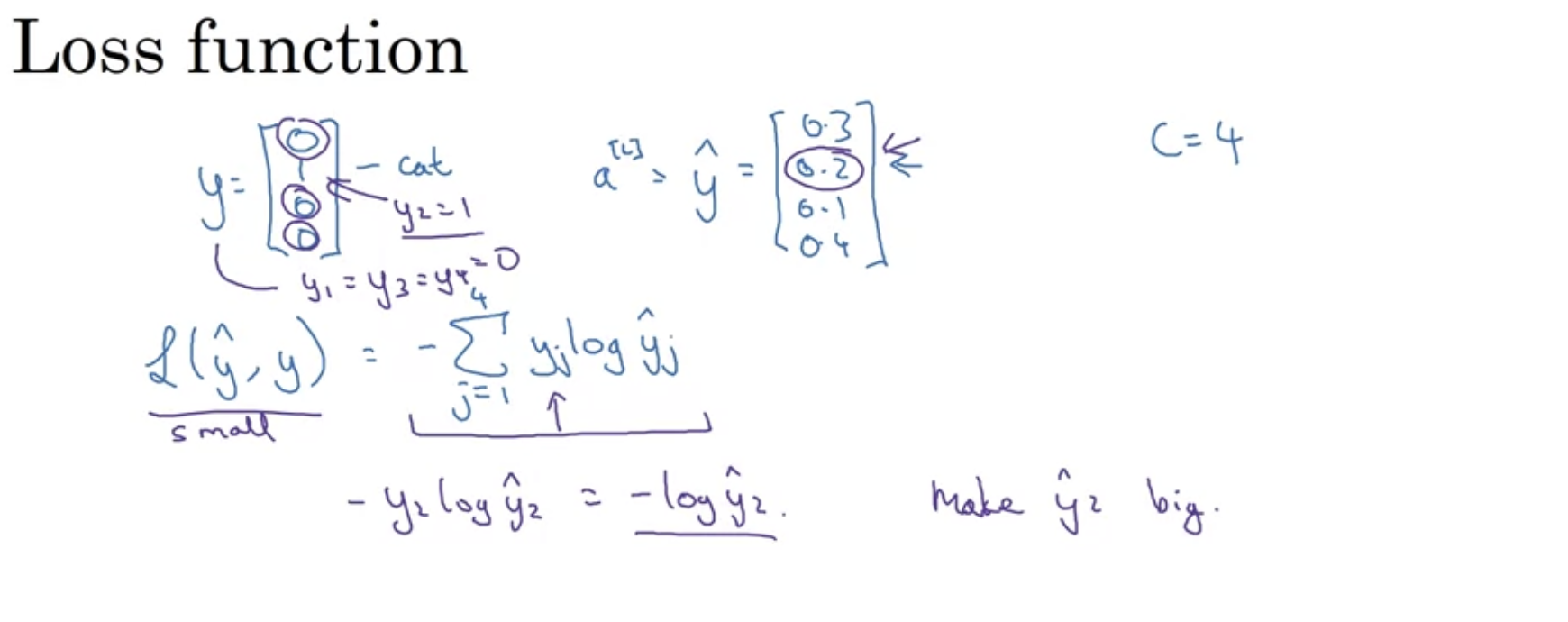
softmax를 적용한 경우에 loss function은 어떻게 계산해야할까? 2번째가 실제로 고양이인 경우, y hat에서 2번째 확률이 가장 커야 한다. 비용함수 식을 보면, 1, 3, 4번째는 y값이 0이므로 더해지지않고, y2 값에 대해서만 줄어들게 된다. 따라서 loss를 줄이기 위해서는 두번째 y hat의 값을 최대한 높여야 할 것이다. 그러한 방향으로 학습이 진행된다.

여러개의 훈련예제를 구하기위해서는, 각 손실을 구하고 평균을 내면 된다.

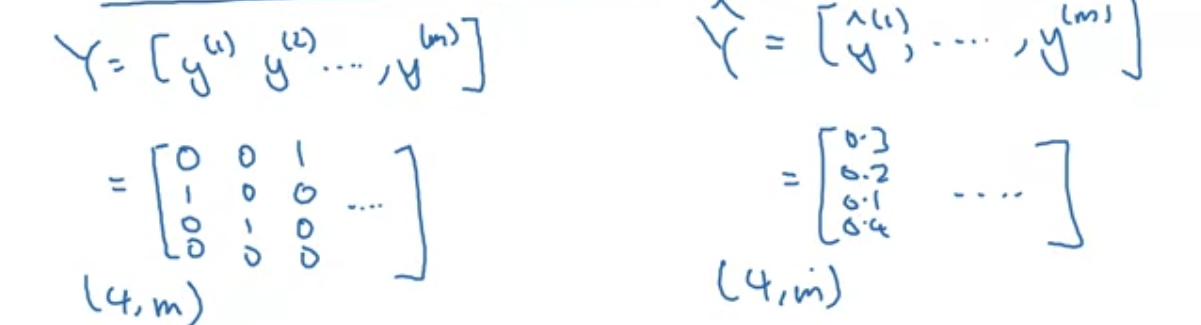
m개 훈련예제에 대해 Y, Yhat에 저장되는 방식은 위와 같다.

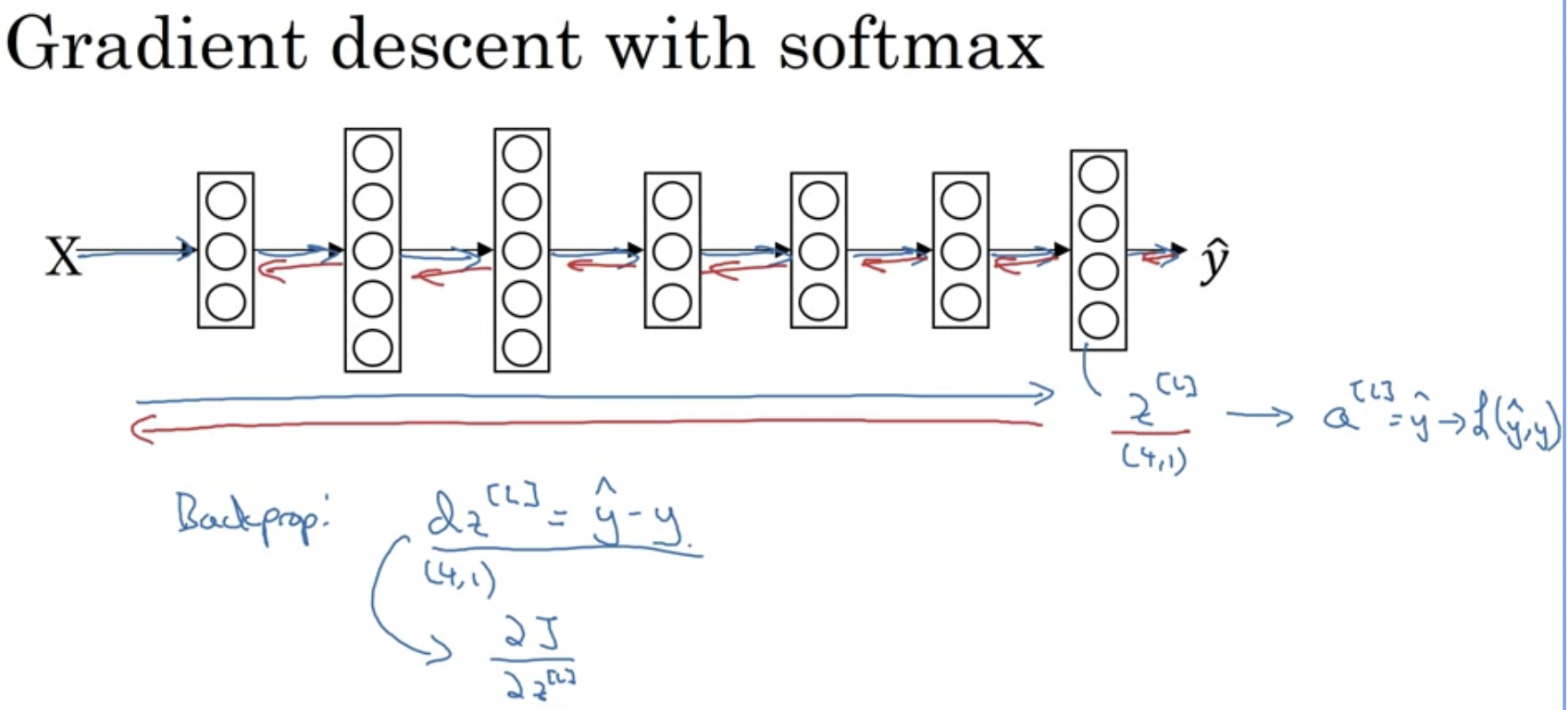
softmax를 적용한 신경망일 경우, 역전파는 어떻게 구성이 될까?

 

실제로 미분하면 나오겠지만, dz = y_hat - y이다. 알아두면 좋다.

이번 프로그래밍 예제에서도 하겠지만, framework를 사용하는 경우, 순전파만 잘 구현을 해주면 역전파는 알아서 구현을 해준다고 한다.

 

Deep Learning Frameworks

지금까지는 파이썬, numpy를 이용하여 처음부터 딥러닝 알고리즘을 구현하는 방법을 배움으로써 실제로 어떻게 동작하는지를 배워보았다.

그러나, 더 복잡한 모델(CNN RNN ..)을 구현할 때에는 처음부터 직접 구현하는 것은 실용적이지 않다. 이를 구현하는데에 도움이 되는 프레임워크가 많이 존재한다.

 

위와 같이 다양한 딥러닝 프레임워크가 있는데, 프레임워크는 항상 변하고 있으므로 한가지를 너무 믿기보다는, 다음과 같은 기준을 통해 그때그때 선택해서 사용하자.

1. 프로그래밍하기 용이한가
2. 빠른가
3. 완전한 오픈소스인건가 (많은 사람들은 이에 대해 그리 신경쓰지않는데, 중요하다. 처음에 오픈소스로 공개했다가 서서히닫는 경우도 있었다.)

 

TensorFlow

예를 들어 위와 같이 cost 함수를 정의한다고 가정해보자.

여기서 cost 함수가 최소화되는 지점이 5임을 쉽게 알 수 있을 것이다. 텐서플로우를 이용해서 최소값을 구해보자.

 

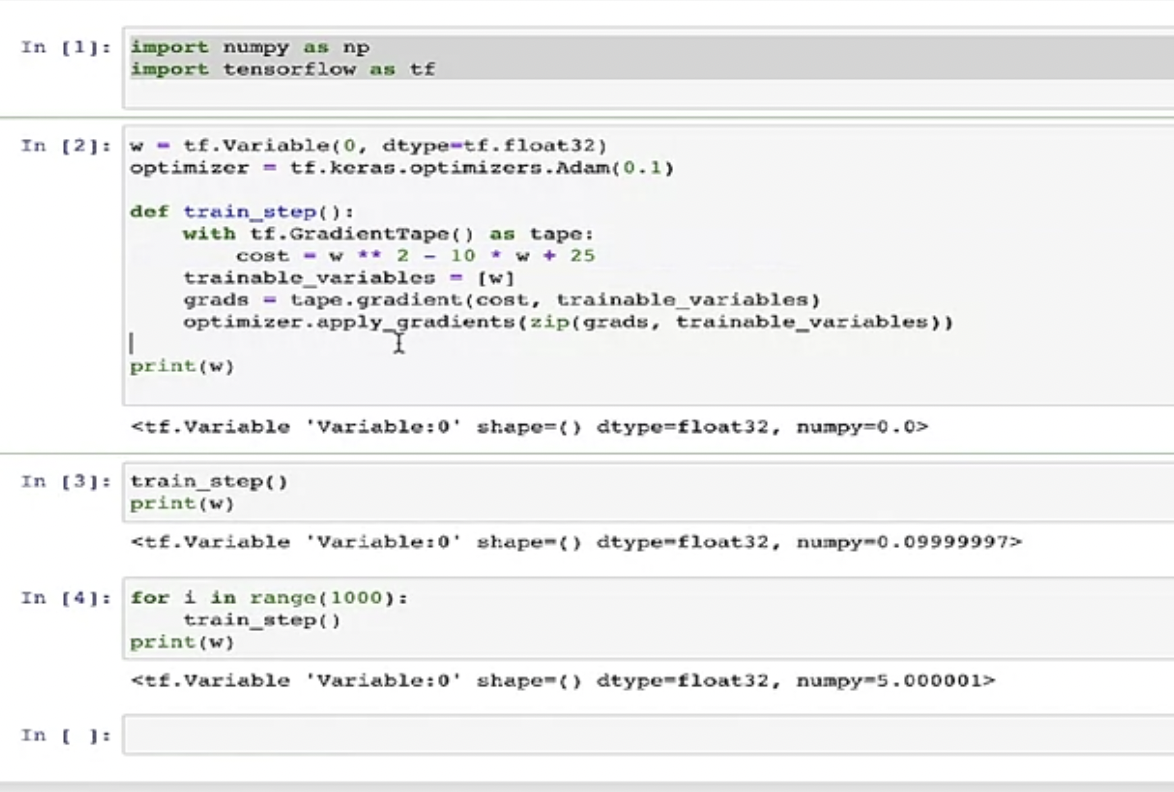
train할 variable에 대해서 tf.Variable로 정의해준다.

Adam 최적화에 대해서도 tf 라이브러리에 있다.

텐서플로우에 있는 tape기능은 cost를 계산하고 그 값을 저장한 뒤, 거꾸로 실행할 수 있게 해준다. 따라서 역전파를 계산하지 않고 순전파만 전개해도, 자동으로 그 역값을 알 수 있다.

최종적으로 5가 나옴을 볼 수 있다.

 

더 간단하게 짤 수도 있다. cost_fn을 인자로 전해줘서 자유롭게 구성할 수 있고, optimizer.minimize에 인자로 cost function을 넣으면 위 값들을 안넣어도 알아서 forward, backward를 진행해준다.

 

참고

https://hyeongminlee.github.io/post/bnn002_mle_map/

Maximum Likelihood Estimation(MLE) & Maximum A Posterior(MAP) | Hyeongmin Lee's Website

(이번 주차 강의랑 직접적인 관련이 있는 것은 아닌데, MLE에 대해 잘 설명해주고 있어 첨부한다. )