*다음 내용은 Andrew ng의 Deep Learning Specialization 과정 중 일부 강좌를 정리한 강의 노트입니다. 틀린 내용이 있다면 말씀해주세요.
Neural Network Representation
윗첨자 대괄호 : 어떤 레이어에서 왔는지 명시적으로 나타낸다.
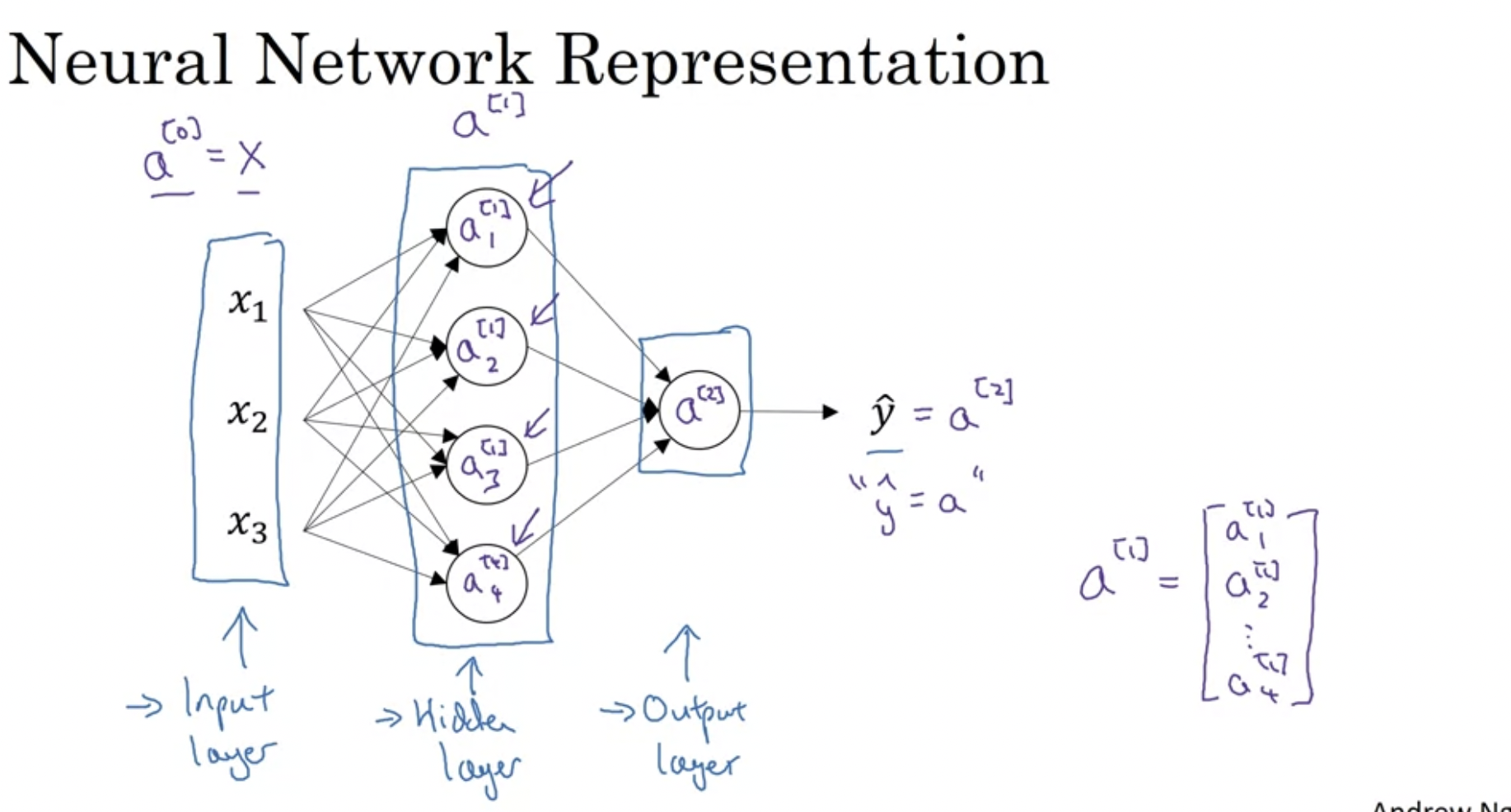
a[0] = X (input layer)
a[1] (hidden layer) → n * 1 행렬 형태
=> layer을 의미하는 것은 위 첨자인 []이고, 한 layer에서 순서를 의미하는 것은 아래 첨자이다.
a[2] → 실수
위 이미지에 있는 것을 2 layer NN이라고 한다. 왜냐하면 신경망에서 보통 레이어를 계산할 때 입력층은 계산하지 않기 때문이다.
그리고, hidden layer와 output layer에서는 연관된 매개변수가 있다.
hideen layer → w, b와 연관됨 (w[1], b2[1])
output layer → w[2], b[2]
Computing a Neural Network's Output
신경망의 output, 즉 출력 결과를 어떻게 계산하는지 구체적으로 살펴보자.
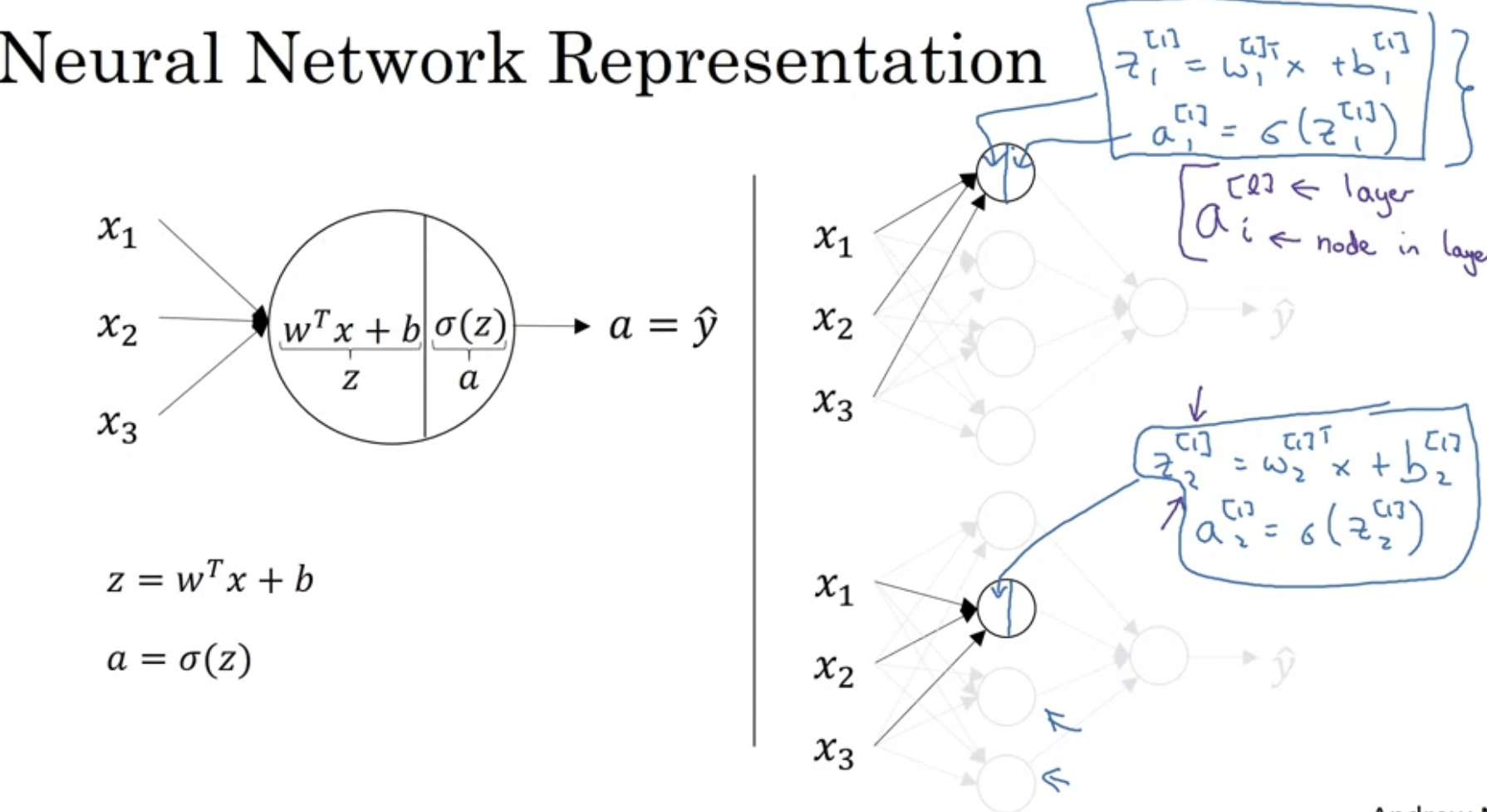
왼쪽이 우리가 아는 계산 방식(logistic regression). 오른쪽은 이 계산을 여러 번 반복하는 것이다.
a에 위 대괄호는 레이어 번호, 및에 아래 첨자는 한 레이어에 있는 노드 번호이다.
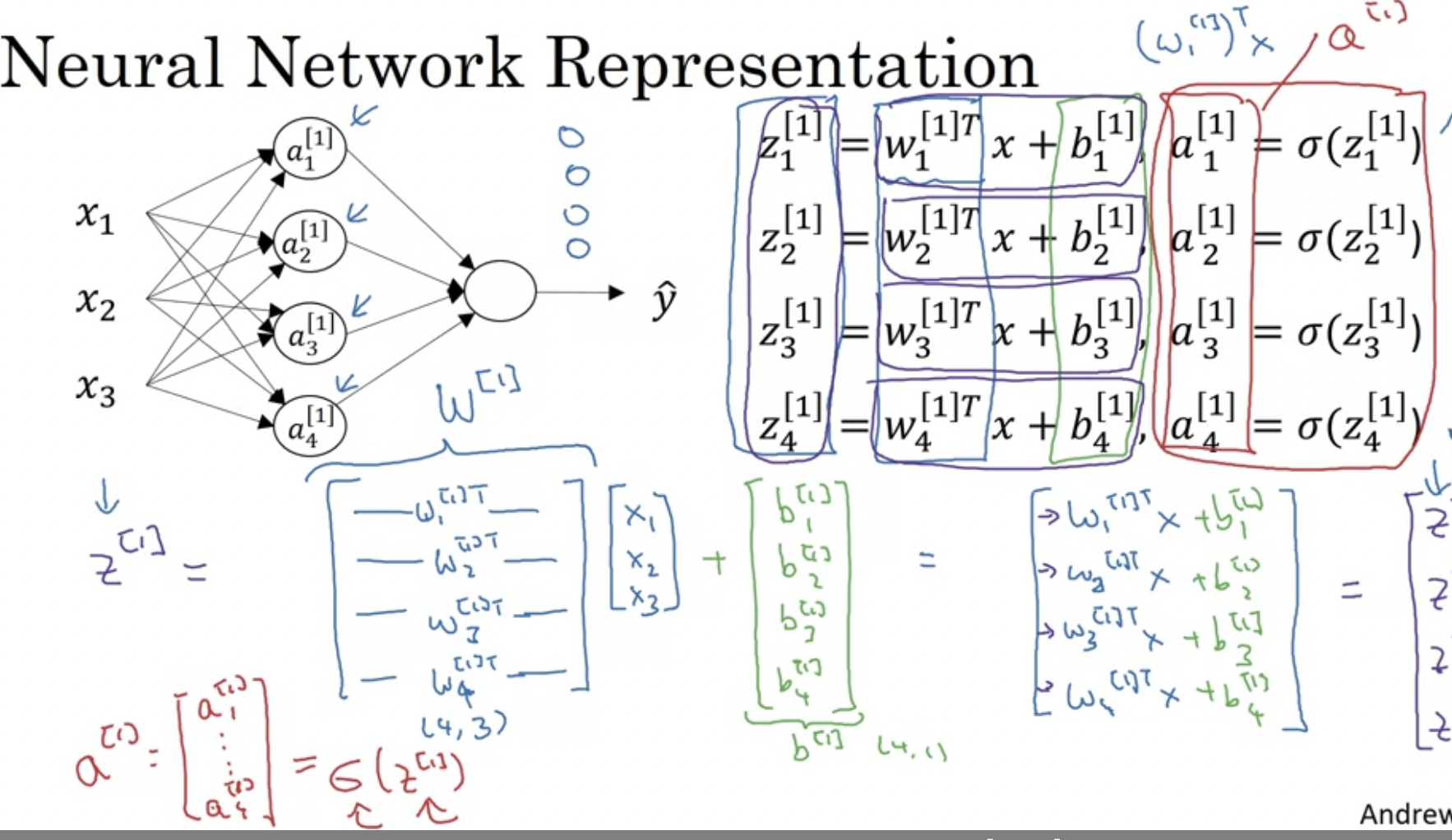
이전 영상에서 배웠다시피, 이것을 벡터화할 수 있다.
w1[1]T값들은 모두 행렬 벡터가 되므로, 레이어 내의 노드가 다른 경우 수직으로 쌓을 수 있다. (vertically stack)
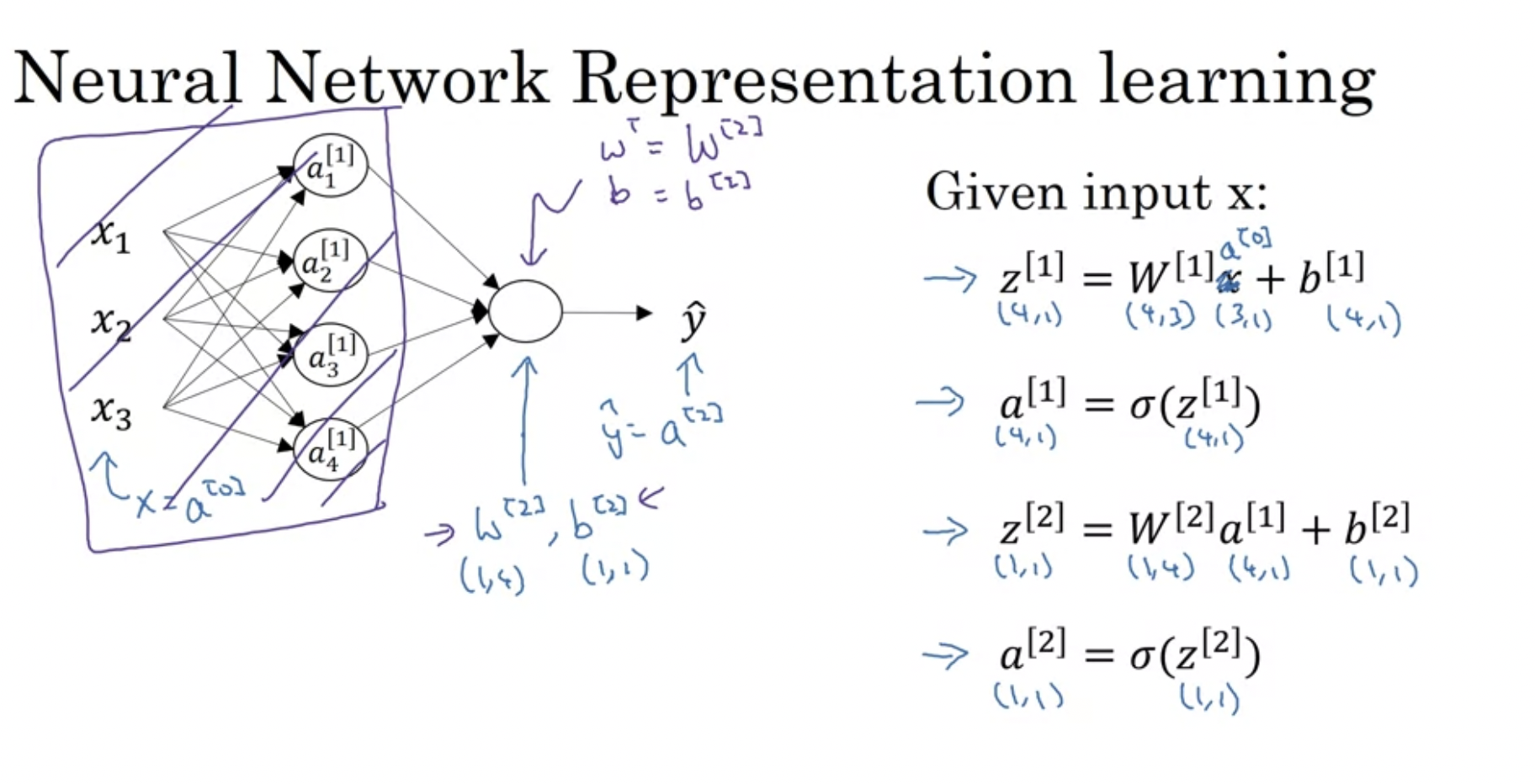
hidden layer를 생각하지 않고, 상위 노드를 보면 우리가 아는 로지스틱 회귀와 유사하다.
대신 w.T를 w[2]라고 하고, b를 b[2]라고 할 뿐이다.
위 이미지에 나온 차원 계산을 풀어서 생각하면 다음과 같다.
w[1].shape → (4, 3)
3개 입력에 대한 weight, 그리고 노드의 개수.를 전치하였으므로, (4, 3)이 된다.
a[0].shape → (3, 1)
a[0] = [x1,
x2,
x3]
으로 구성된다. 따라서 (3, 1)임.
b[1].shape → (4, 1) → 4개 노드에 따른 값을 수직으로 이어붙였으므로.
sing input feature vector a가 들어갔을 때, 뉴럴 네트워크에서 어떻게 계산되는지를 살펴보았다. training example을 stacking함으로써 한번에 계산할 수 있다.
Vectorizing Across Multiple Examples
지난 영상에서는, 단일 훈련 예제를 사용하여 신경망을 예측하는 방법을 살펴보았다. 이 영상에서는 여러 훈련 예제에서 벡터화하는 것을 살펴볼 것이다. 다음과 같이 여러개의 훈련 예제가 있을 때,

m개의 훈련예제가 있을 때, 우선 각각의 훈련 예제를 [layer number][example i]로 표현해보자.
이것 또한 지난 주차에 살펴본 것처럼 벡터화가 가능하다.
nx개의 입을갖고 있는 훈련 예제가 m개있을 때, 다음과 같은 모양이 가능할 것이다. (열벡터를 차곡차곡 옆으로 쌓음)
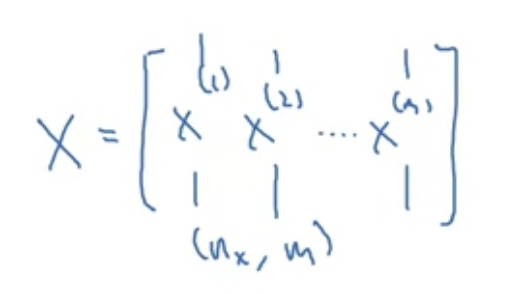
수평으로 쌓으며 훈련 예제에 대한 인덱스화가 가능하다.
수직 인덱스는 신경망의 다른 노드(different input feature), 수평 인덱스는 다른 훈련 예제들을 의미한다.

벡터화로 뉴럴 네트워크 구성한 모습은 위와 같다. 다음 강의에서는 이것이 어떻게 가능한지 살펴볼 것이다.
Activation Functions
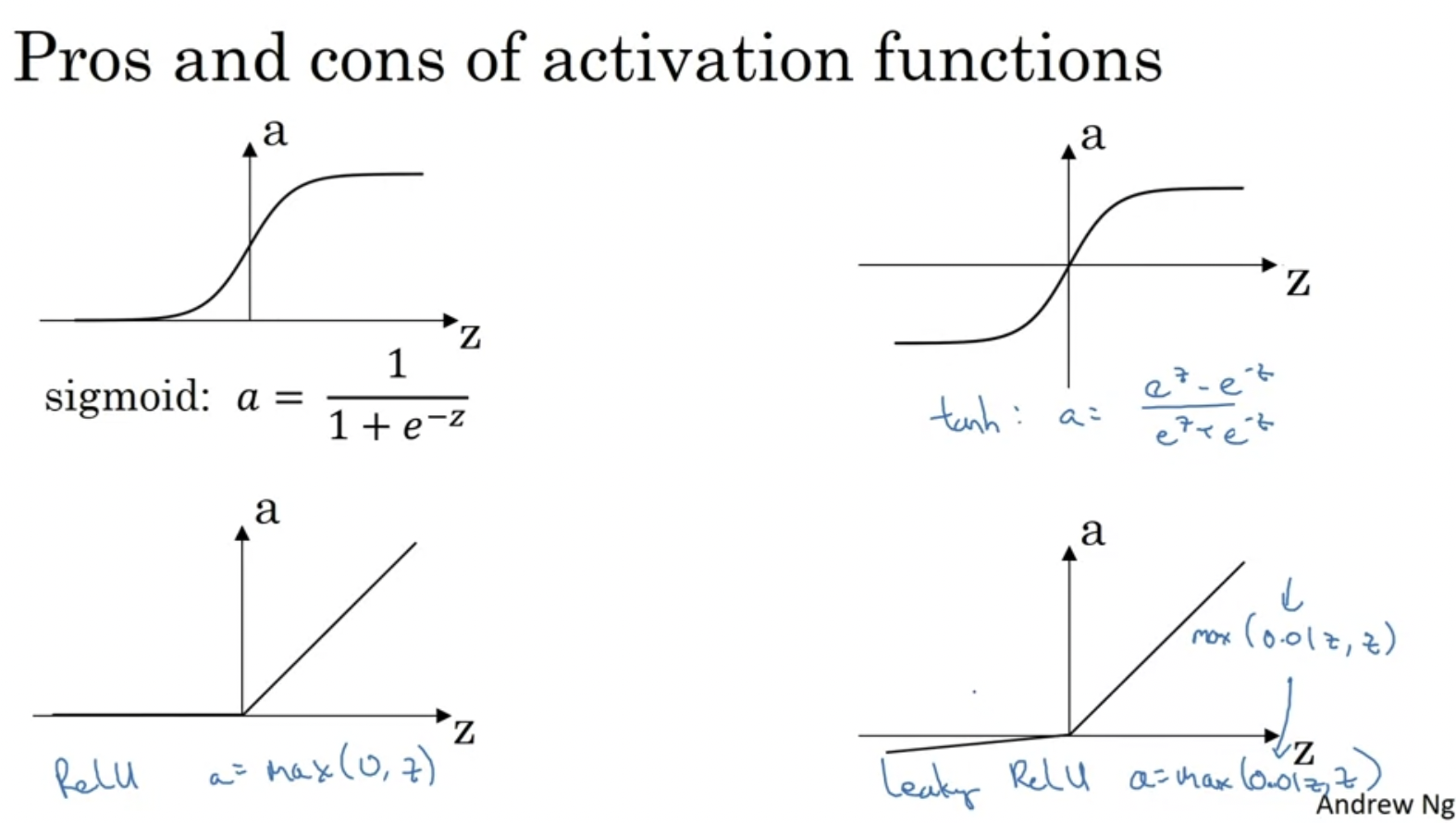
지금까지 다룬 시그모이드 = 활성화함수의 일종
그 외에도 다양한 활성화 함수가 있다.
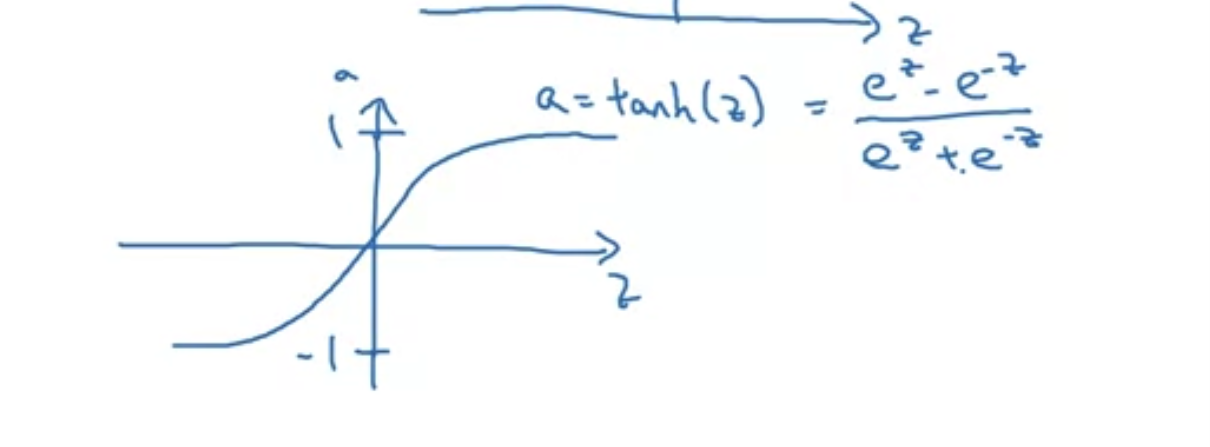
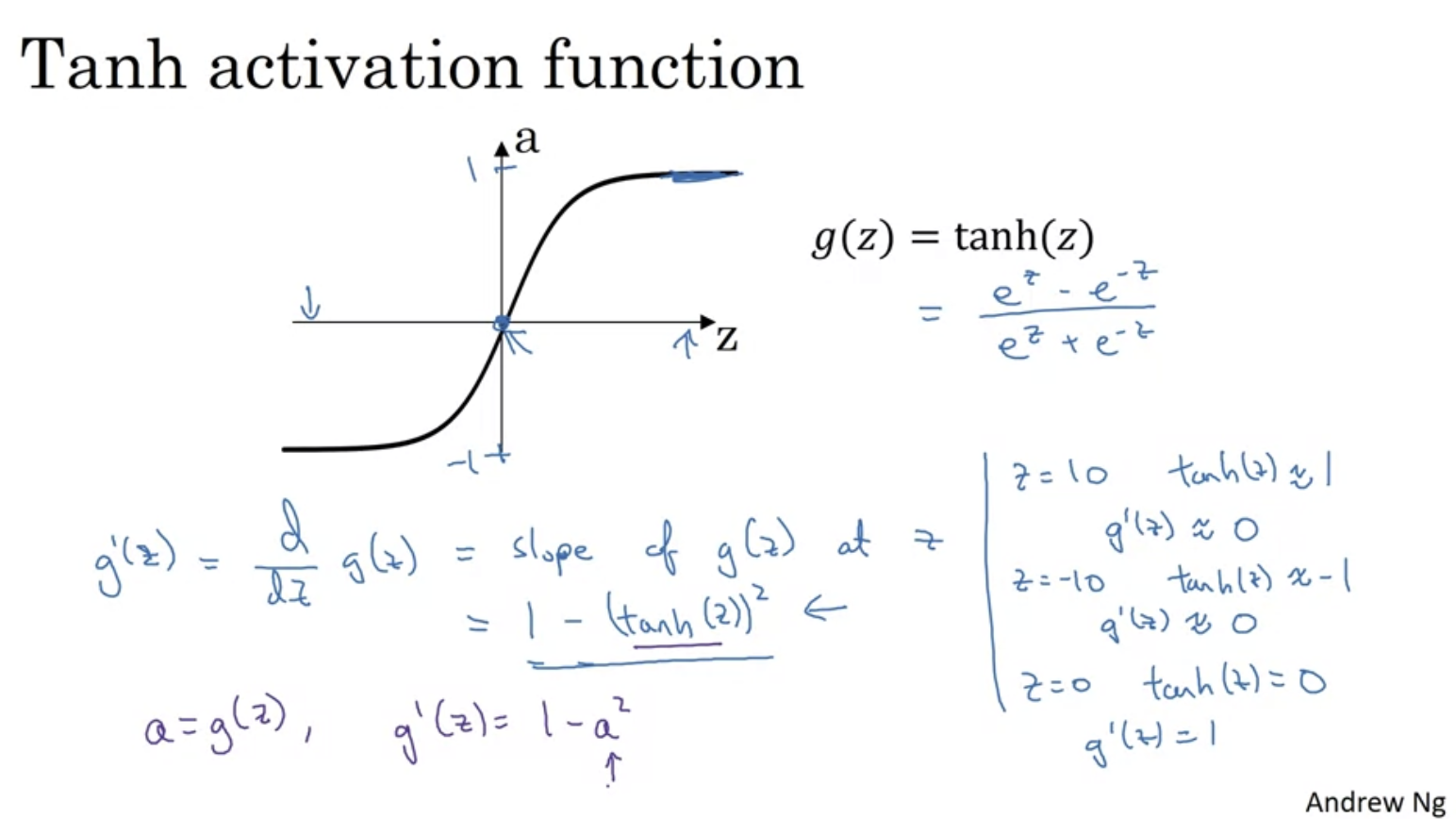
tanh 함수 : 시그모이드 함수 이동버전인데, 보통 시그모이드보다 항상 더 잘 작동한다고 한다. 왜냐하면 범위가 -1, 1이기 때문에 활성화의 평균이 0에 가깝기 때문이다. 따라서 데이터의 평균이 0.5가 아니라 0이 되도록 할 수 있다. 이렇게 하면 다음 레이어에 대한 학습이 더 쉬워진다고 한다. 더 자세한 얘기는 이후 second course에서 다룰 것이다.
보통 tanh 함수가 더 우수하지만 output layer에 대해서는 예외이다. 왜냐하면 최종값인 y hat은 -1과 1사이보다는 0과 1사이에서 출력하는 것이 더 합리적이기 때문이다. 그래서 sigmoid function은 binary classification task에서 upper layer에서 주로 사용한다.
활성화함수는 레이어마다 다를 수 있다. (e.g. layer 1에서는 tanh 함수 사용하고, layer 2 (output layer)에서는 sigmoid 함수 사용)
sigmoid 함수, tanh함수 단점 : z가 매우 크거나 매우 작으면 도함수가 매우매우 작아진다는 것이다. 그러면 기울기가 0에 가까워지므로 기울기 하강 속도가 느려질 수 있다.
⇒ 이러한 문제 때문에 ML에서 ReLU가 매우 선호된다.
ReLU는 z가 정확히 0일 때 문제가 생길 수있지만, 컴퓨터에서 z가 0.0000000000000000..이 될 확률은 매우 낮다.

다양한 활성화 함수 중에 선택하는 tip
- 출력값이 0, 1이고 이진 분류를 사용하는 경우 → 시그모이드 활성화 함수
- ReLU → default choice임
- 가끔 tanh쓰기도.
- ReLU의 단점은 z가 음수일 때 도함수가 0이 된다는 것. 그래도 잘 작동한다. 그리고 Leaky ReLU도 있다고 한다. ReLU보다 값이 괜찮은데 실전에서 잘 사용하지는 않는다.
*leakly ReLU : z가 음수일 때 0이 아니라 아주 작은 값을 주는 함수이다. ReLU의 변형버전
ReLU, leaky ReLU : 학습 속도가 훨씬 빠르다는 장점이 있다. 기울기가 0이 되는 상황이 잘 일어나지 않기 때문이다.
Why do you need Non-Linear Activation Functions?
왜 non linear activation function을 사용해야할까?
만약 활성화 함수가 linear(i)하다면, 즉 아래 그림처럼 z를 받았을 때 z를 그대로 출력한다면 어떻게 될까?
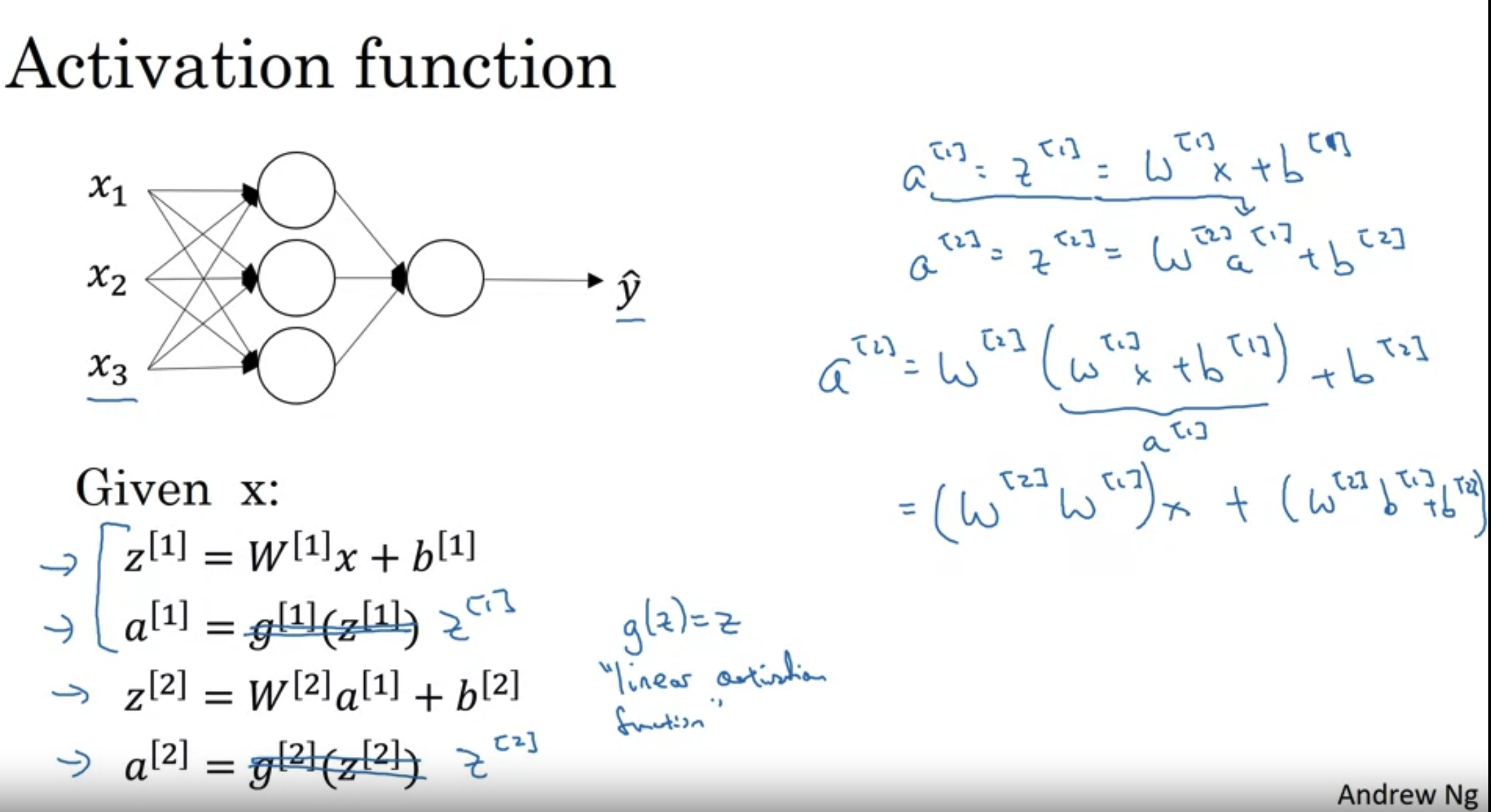
hidden layer, 즉 deep neural network이 의미없어진다. 여러 layer을 계산하든 한 layer을 계산하든 값이 똑같기 때문이다.
→ layer의 수와 상관없이 많은/복잡한 계산을 할 수가 없다.
linear activation의 경우 한 번 정도 사용할 수 있는데, 보통 output layer에서 그대로 출력할 때 사용하지, hidden layer에서는 보통 잘 사용하지 않는다.
non linear activation을 사용하는 이유에 대해 알아야 한다.
Derivatives of Activation Functions
활성화 함수를 이용할 때, 우리는 활성화함수의 기울기를 계산해야 한다. 이번 강의에서는 기울기를 계산하는 방법에 대해 알아보겠다.
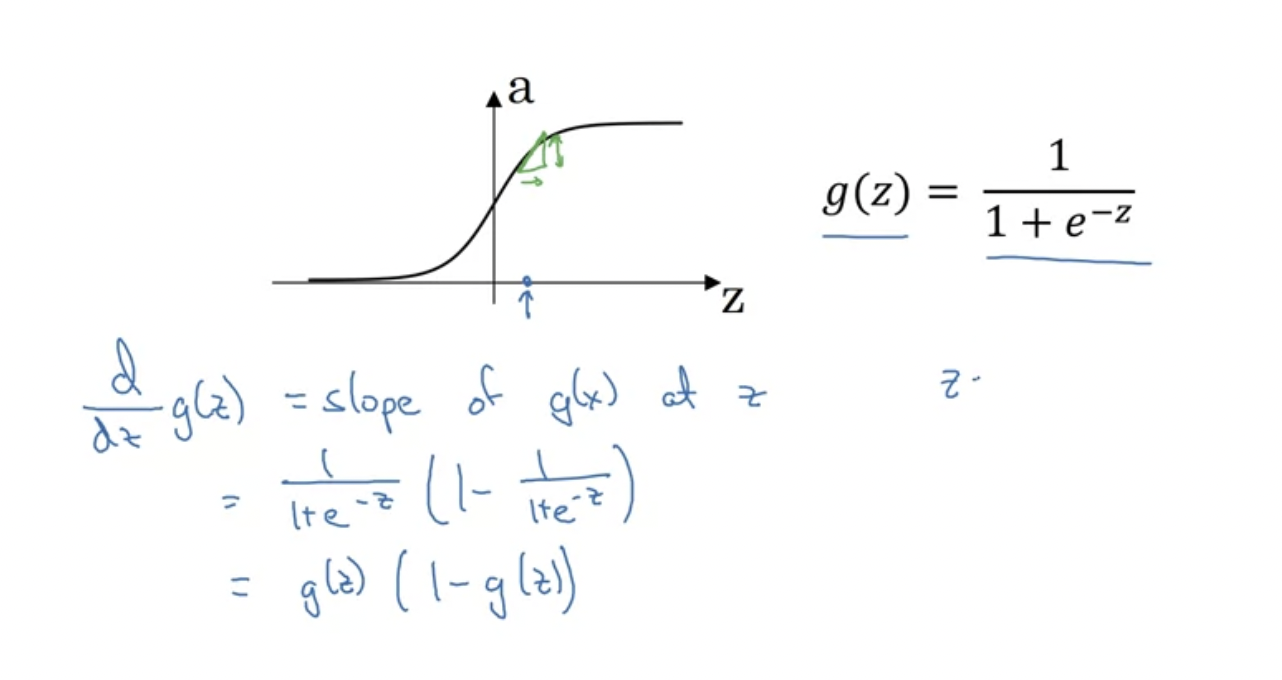
우리가 잘 아는 시그모이드 함수 g(z)의 기울기를 구하면 g(z)(1 - g(z)가 나온다.
z가 매우 클 때와, 매우 작을 때 기울기가 0애 가까워짐을 도함수를 통해 확인할 수 있다. 반면 z=0일 때 g(z)는 1/2이고, 그래서 도함수는 1/4가 된다.
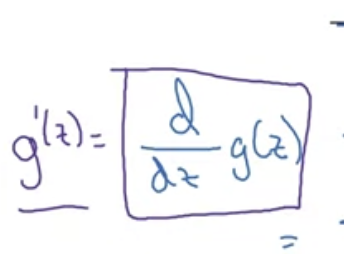
위 이미지에서 왼쪽과 오른쪽은 같은 것을 의미한다.
g(z)를 a로 보면, 도함수는 a(1-a)이다. 이것의 장점은, 이미 g(z)에 대하여 계산을 마쳤을 경우 (마친 다음 a로 저장하였을 경우) 도함수도 매우 빠르게 계산이 가능하다는 것이다.
다음은 tanh(z)의 함수 및 기울기이며, z를 최대로 늘이거나 최소로 줄여보면서 확인해볼 수 있다.
다음은 ReLU함수의 기울기이다.
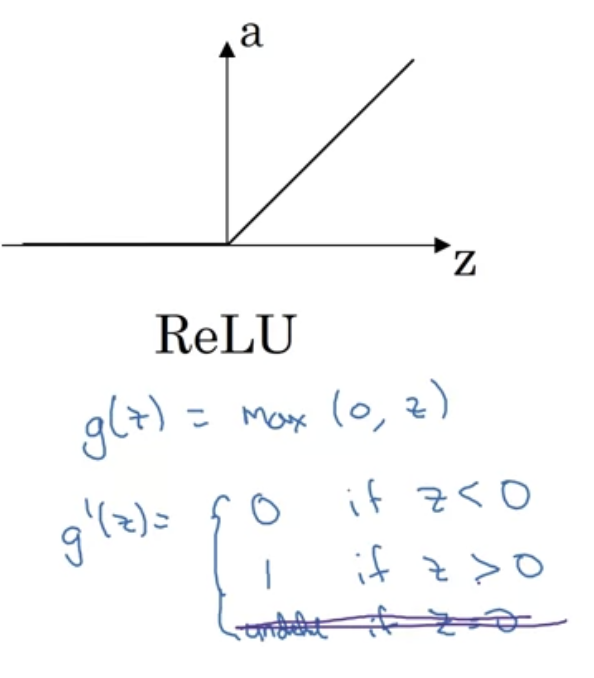
보통 정확히 0이 경우에는 (실제 구현에서는 완벽이 0일 일은 없긴 하다) 그냥 1로 둔다. 다음은 Leaky RELU이다.
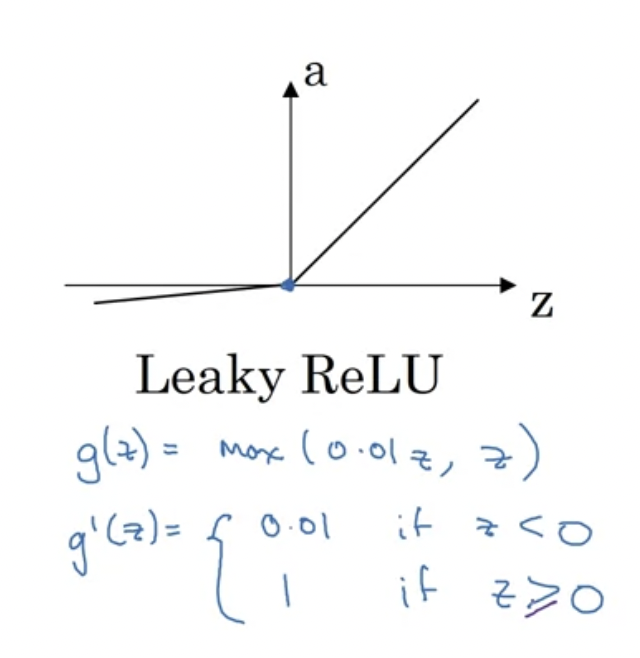
Gradient Descent for Neural Networks
앞에서 도구들을 다 배웠으니, 이번에는 신경망에서 hidden layer를 통한 Gradient descent를 구해보자

쉽게 말하면, 우리가 전 주차에서 했던 logistic regression을 반복하는 것이다.
여러 layer을 사용하게 되면서 순전파와 역전파의 개념이 나온다.
순전파(forwards propagation) : 뉴럴 네트워크의 그래프를 계산하기 위해서 중간 변수들을 순서대로 계산하고 저장. 즉, 입력층부터 시작해서 출력층까지의 순서로 처리됨
역전파(back propagation) : 중간 변수와 파라미터에 대한 그래디언트(gradient)를 반대 방향으로 계산하고 저장
딥러닝 모델을 학습시킬 때, 순전파(forward propagation)과 역전파(back propagation)는 상호 의존적
역전파의 식 전개는 아래와 같다.
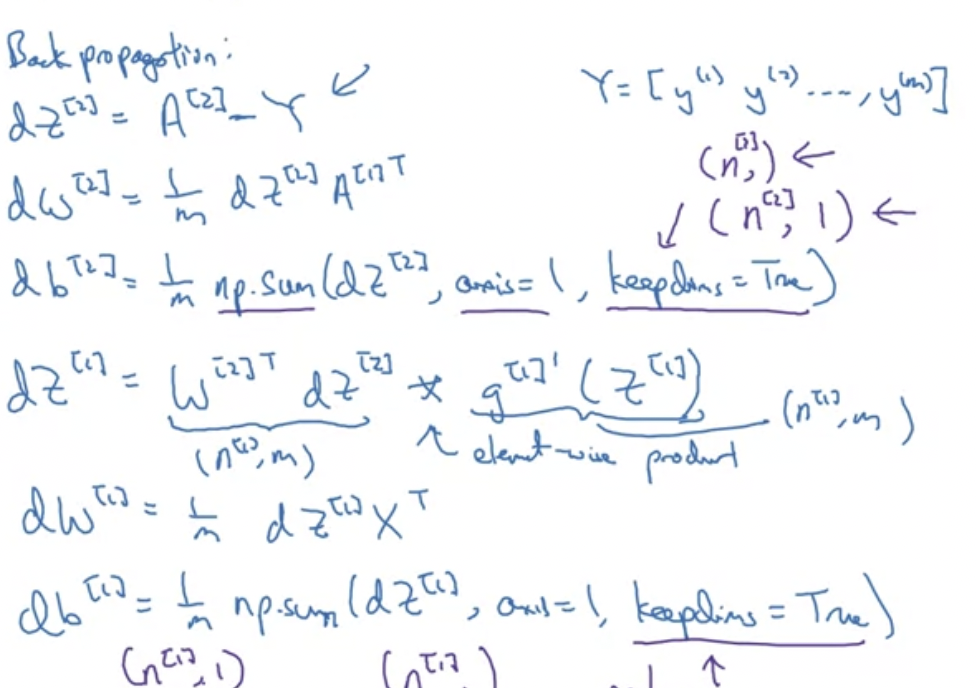
해당 영상에서는 왜 다음과 같은 식이 도출되었는지에 대해 증명이 나오진 않는다. 관련 영상은 (optional) 영상에서 따로 증명하고자 한다. 코드를 작성하는 면에 있어서는 몰라도 아무 지장 없다고는 한다.
Random Initialization
신경망을 변경할 때는, weight(가중치)를 랜덤으로 초기화하는 것이 중요하다.
로지스틱 회귀의 경우, 가중치를 0으로 초기화해도 괜찮다. 그러나 neural network(신경망)에서 파라미터를 모두 0으로 초기화하고, 그래디언트 디센트를 적용하면 작동하지 않는다.
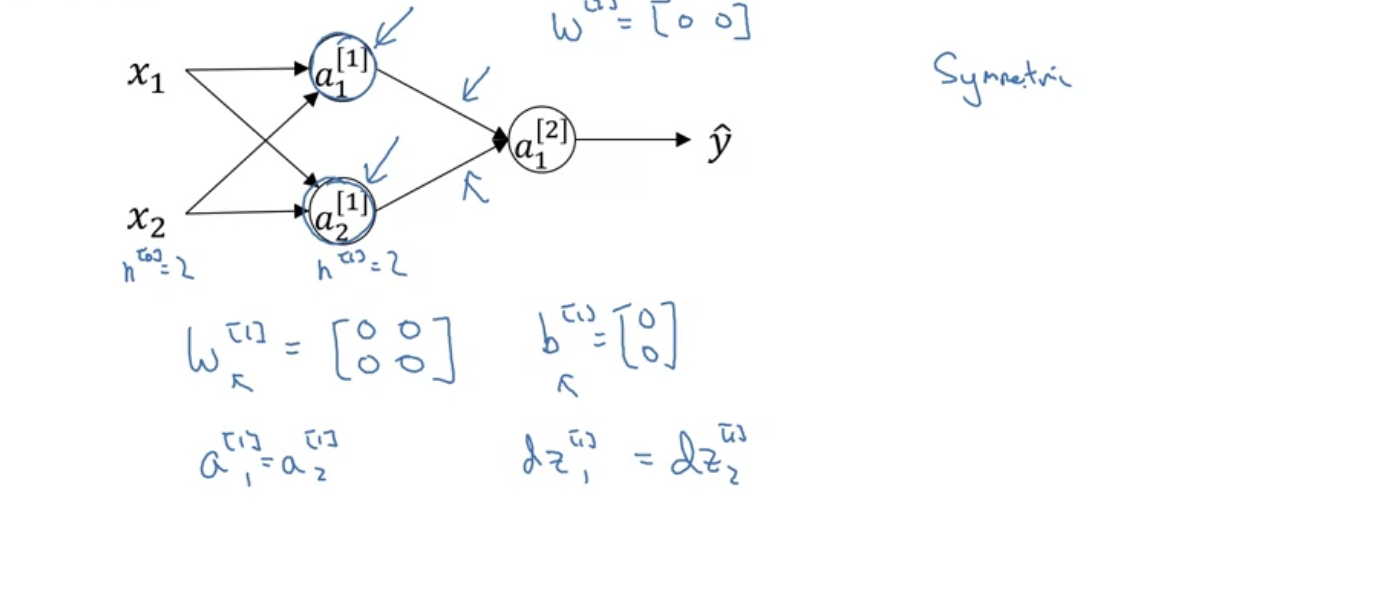
만약 W 행렬을 모두 0으로 초기화하면, 입력값과 상관없이 항상 똑같은 값을 가지게 될 것이다.
그 말은 a1 = a2이며 dz1 = dz2이다. (곱하면 다 0이므로)
그렇다면 훈련을 반복하더라도 이 hidden layer은 계속 동일한 함수를 계산할 것이다.
그래디언트 디센트를 통해 w을 갱신시키면
w[1] = w[1] - dw * 알파
인데 이 행렬의 첫번째 행과 두번째 행은 같을 것이다.
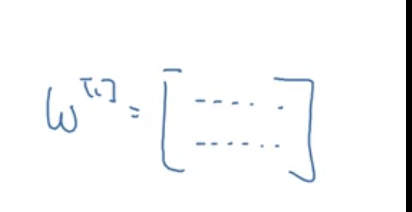
(가중치 행렬의 각 행은 하나의 layer 안에서 각 노드의 값을 가리킨다.)
이렇게 되면 hidden unit은 항상 똑같은 값(symmetric)을 가지게 되므로
layer가 2개 이상 있는 것이 의미가 없어진다.
따라서 이러한 문제를 해결하기 위해 (symmetry breaking problem) 파라미터를 무작위로 초기화해야 한다. 다음과 같은 방식으로 하면 된다.
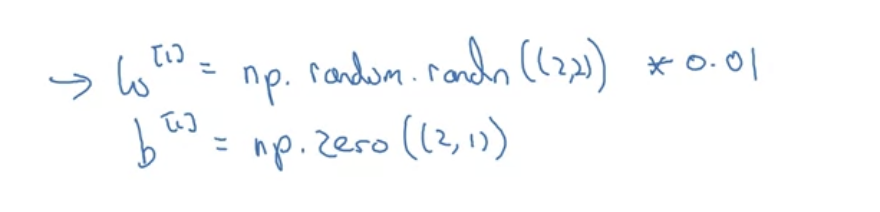
보통 작은 값으로 만들기 위해 np.random을 한 후 매우 작은 값을 곱한다. b는 0으로 초기화해도 상관없다는 사실이 밝혀졌기 때문에 그냥 0으로 초기화해도 괜찮다.
그렇다면 가중치를 왜 작은 값으로 초기화할 까?
→ 왜냐하면 sigmoid, tanh와 같은 활성화 함수를 사용하는 경우, 가중치가 너무 크면 기울기가 0에 가까워질 확률이 크다. (너무 크거나 너무 작을 때) 그렇게 되면 기울기 하강이 매우 느리게 이루어질 것이다.
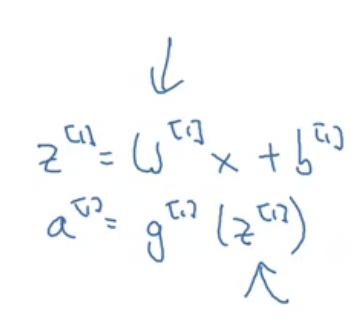
요약 : w값이 매우 큰 경우, z값 또한 클 확률이 높고 그러면 활성화함수를 적용할 때 역전파 과정에서 학슴 속도가 매우 느려진다. 따라서 보통 작은 값을 곱해준다.
그런데, 매우 deep neural network을 훈련시킬 때는, 0.01 말고 다른 값을 곱하고 싶어질 것이다. 그것이 무엇인지는 다음주에 다룰 것이다.
참고
https://ko.d2l.ai/chapter_deep-learning-basics/backprop.html
3.14. 순전파(forward propagation), 역전파(back propagation), 연산 그래프 — Dive into Deep Learning documentation
ko.d2l.ai
'Deep Learning Specialization 강의 > Neural Networks and Deep Learning' 카테고리의 다른 글
| Deep Neural Networks (4주차) 정리 (0) | 2024.07.11 |
|---|---|
| Logistic Regression as a Neural Network (2주차) 정리 (0) | 2024.07.08 |
| Introduction to Deep Learning (1주차) 정리 (2) | 2024.07.03 |
