*다음 내용은 Andrew ng의 Deep Learning Specialization 과정 중 일부 강좌를 정리한 강의 노트입니다. 틀린 내용이 있다면 말씀해주세요.
이번주차는 DNN에 대해 배우는데, 사실상 지금까지 배운 shallow neural network를 반복한 것이기 때문에 지금까지 배운 것의 반복이라고 보아도 무방하다.
Deep L-layer Neural Network
이번 주차의 목표: 3주차동안 배운 아이디어를 묶어서 나만의 심층 신경망을 구현하는 것

logistic regression : very "shallow" model
1 hideen layer = 2 layer NN (hidden layer, output layer)
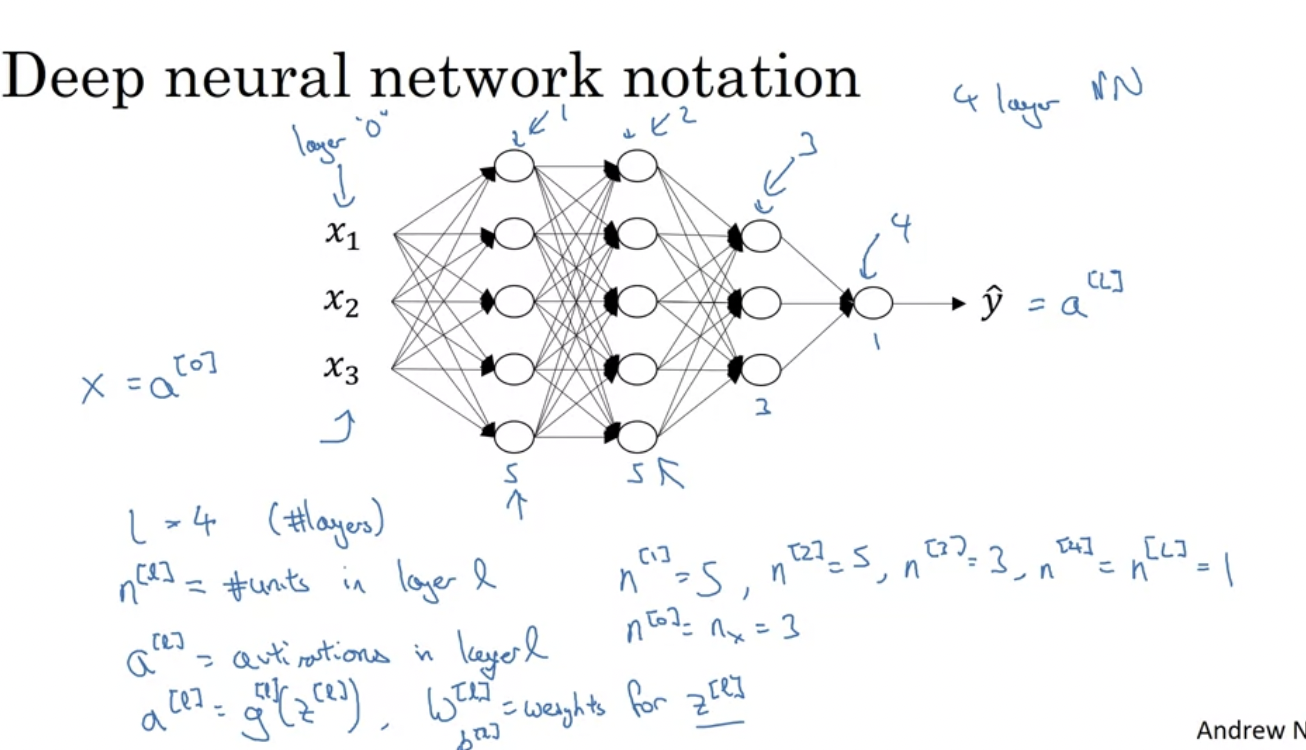
<DNN에서의 표기법(notation)>
L ← 네트워크의 레이어 수를 나타낸다.
n ← 특정 레이어의 유낫의 수를 나타낸다.
Forward Propagation in a Deep Network

All the training examples are column vectors stack left to right.
=> 행렬을 구성할 때, layer node는 위에서 아래로 (수직으로) 쌓이고, train example은 왼쪽에서 아래쪽으로 (수평으로) 쌓인다.

오른편과 같이 식을 쓰고, 레이어마다 for loop을 돌리며 이를 반복한다.
우리는 neural network을 구성할 때, 가능하면 최대한 for loop code를 없애야 한다고 배우긴 했다. 하지만 layer 별 계산의 경우 어쩔 수 없이 for loop을 돌릴 수 밖에 없다. (내 추측 : 그 이유는 각 layer마다 노드의 수가 다르고, 순전파 역전파 모두 이전 layer의 결과를 기반으로 하여 다음 layer을 계산하기 때문이다.)
딥뉴럴네트워크를 돌리는 것은 결국, 이전에 다룬 얕은 뉴럴 네트워크를 여러 번 반복하는 것
→ 버그를 줄이기 위해서는 기존 네트워크의 matrix dimension에 대해 주의깊게 생각하는 것이 필요하다.
Getting your Matrix Dimensions Right
우선 아래 신경망은 단일 예제에 대해서 다루고 있다.

z[1] → 첫번째 hidden layer에서 활성화 함수를 적용한 벡터이다 . (3, 1)
w[k] = (n[k], n[k -1 ]) 차원을 가진다. 왜냐하면 함께 곱해지는 A[k-1]는 (n[k-1], 0]
dw 또한 기존 w와 동일한 dimension을 가지므로,
dw[k] = (n[k], n[k - 1])
b[k] = (n[k], 1)
db[k] = (n[k], 1)
*z와 a는 동일한 차원을 가진다. (a는 z에 활성화 함수를 적용한 것이기 때문)
Z[1] → z[1][1], z[1][2] .. z[1][m]까지의 개별 예제들을 합친 것.
따라서 Z[1]는 (n[1], m) (모든 훈련 예제가 수평으로 연결되므로)
X(벡터화된 x) 또한 (n[0], m)이고, b[1]는 자동으로 브로드캐스팅이 되어서
(n[1], 1) → (n[1], m)
z[k], a[k]는 (n[k], 1)이지만,
Z[k], A[k]는 (n[k], m)
dz[k], da[k]또한 같은 차원을 가진다.
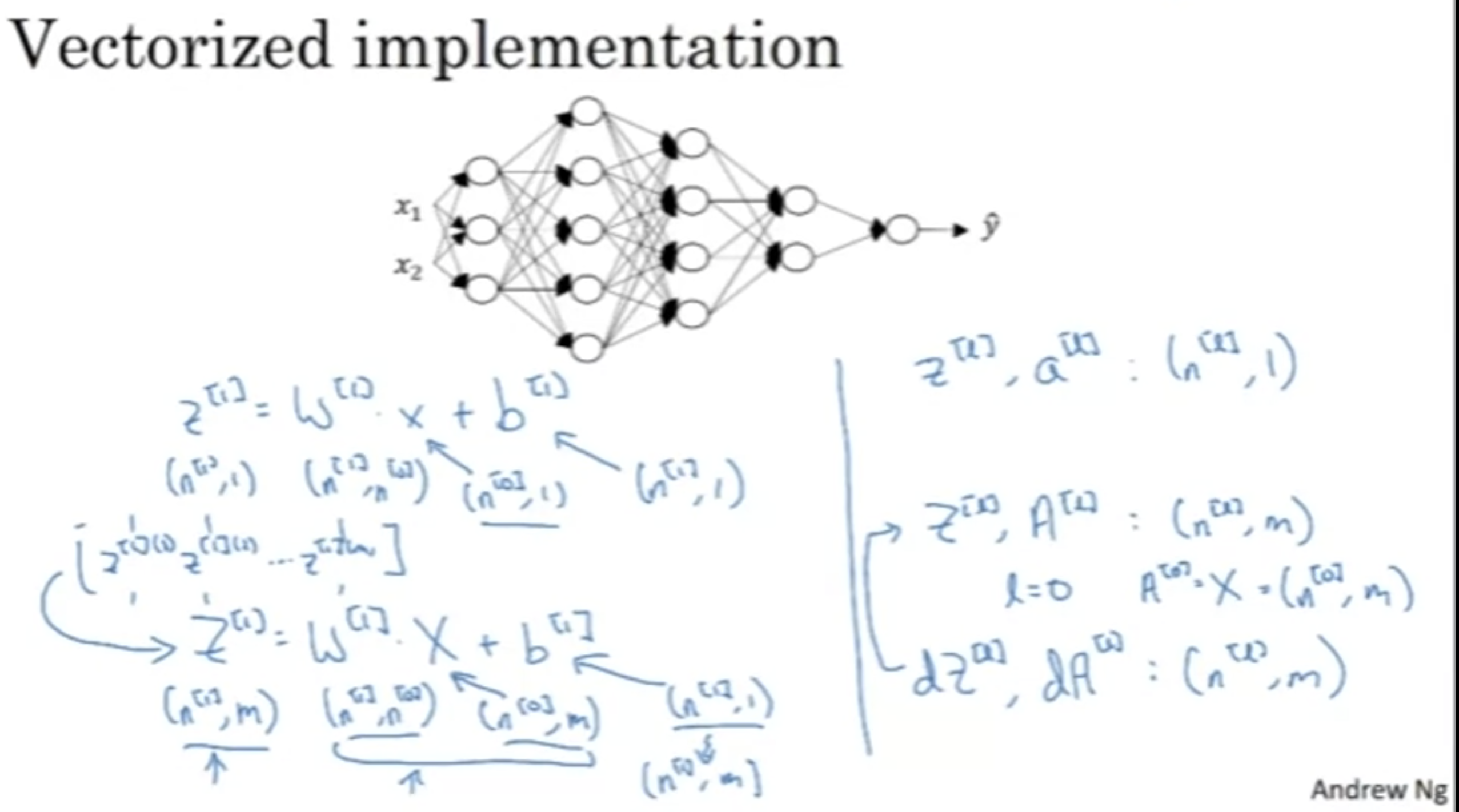
지금까지 배운 내용을 m개의 훈련 예제로 확장하면 위와 같다.
Why Deep Representations?
deep neural network가 shallow neural network보다 효과적인 이유가, 단지 신경망의 크기때문은 아니다. 몇가지 예를 살펴보자.

deep neural network(직관적 설명) : 초반 layer가 low level의 간단한 특징을 학습한 다음, 더 깊은 layer에서 간단한 특징을 조합하여 특정 단어를 인식하거나. 문장을 감지할 수 있도록 한다. (simple에서 점점 complex해진다. ) ⇒ 이러한 점에서 인간의 뇌와 유사하다.
첫번째 hidden layer은 단지 얼굴의 가장자리 / 방향성만 찾는다. 그러한 다음 이것을 그룹화하여 면의 일부를 형성할 수 있다. (특정 뉴런은 눈을 찾고, 다른 뉴런은 코를 찾는 등..) 그리고 얼굴의 다른 부분을 결합함으로써, 다른 종류의 얼굴을 인식하게 될 수 있다.
음성 인식에서도 적용된다. 초반에는 낮은 파형을 감지하다가 이것을 구성함으로써 소리의 기본 단위를 감지하는 법을 배울 수 있을 것이다.
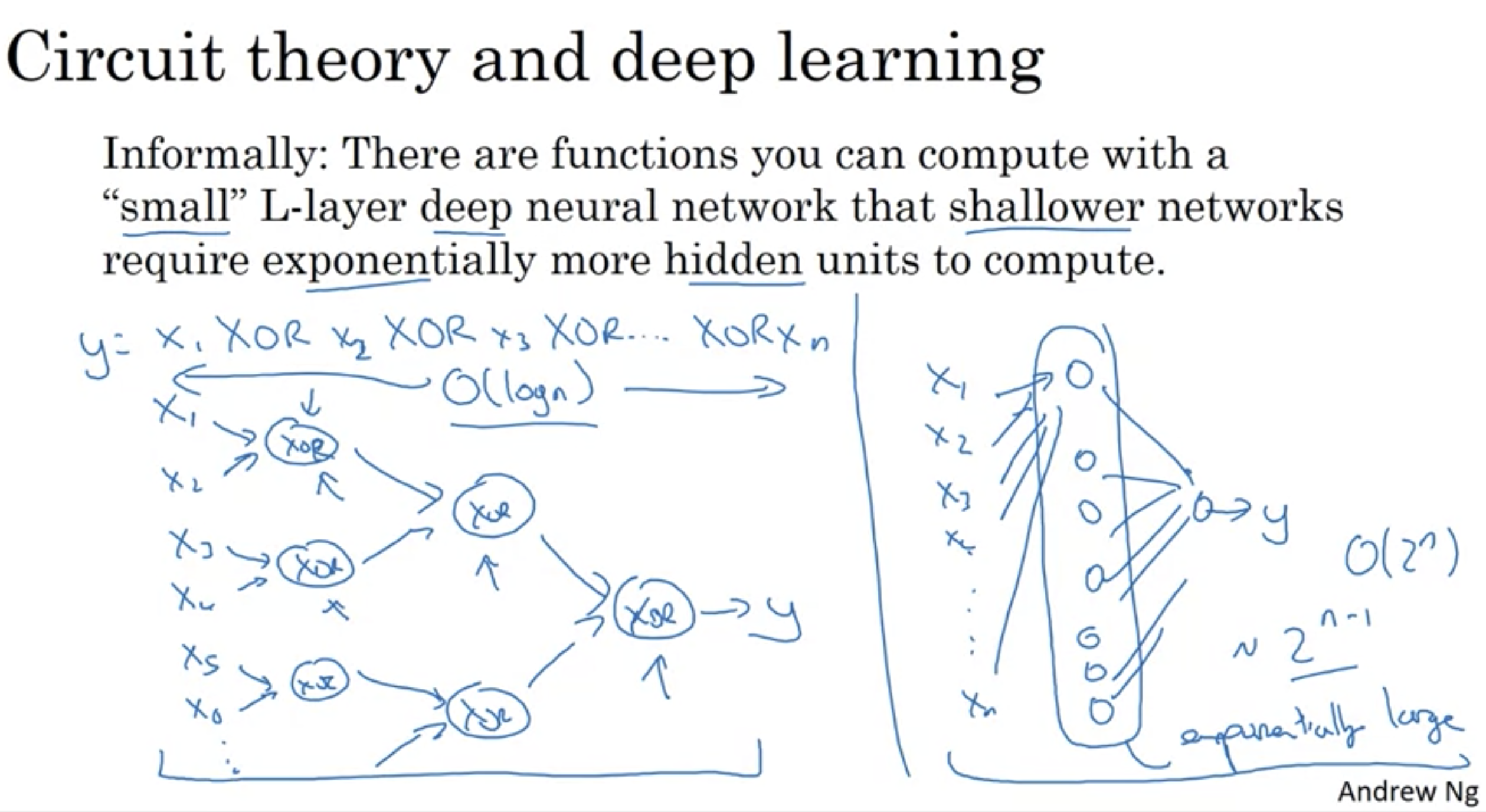
deep neural network를 적용함으로써 문제가 쉬워지는 경우가 있다. 예를 들면, XOR을 계산하기 위한 여러 식이 있는데, 이것을 shallow neural network에서 작성하려면 한번에 이 식들을 넣어야 한다. (즉, 많은 hidden unit이 요구된다.) 왼쪽같이 여러 layer을 사용하면 logn에 가능한데, 오른쪽같이 shallow layer에서 하려면 2^n (지수적)으로 계산량이 요구된다.
ng 의견: 솔직히 딥러닝이 유행한 데에는 이름에서 오는 브랜딩도 있다..그러나 무조건 많은 레이어를 사용하는 딥러닝이 좋은 것은 아니고, 보통 로지스틱 회귀로 시작해서 1~2개의 hidden layer을 시도하고, 이를 매개변수로 사용하여 적합한 깊이를 찾아내고자 한다.
Building Blocks of Deep Neural Networks
기본적으로 우리가 배운 내용을 기반으로 하여, 어떻게 DNN에 적용시킬 수 있는지를 살펴보자.

forward, backward function이 코드 단위에서 어떻게 이루어지는지를 block 단위로 보고 있다.

deep neural network는 위 과정을 반복하면서 진행된다. (gradient descent) 위가 forward, 밑이 backsward)
정리: 각 레이어에는 forward propagation, 이와 상응대는 back propagation, 그리고 정보를 전달할 수 있는 cache가 있다.
implementional detail : 여기서 cache(z값)를 backward propagion을 위해 저장하는 값이라고 생각할 수 있다. 그러나 구현할 때, w1. .b1 또한 parameter로 backward에 주는 것이 편할 것이다. 따라서 실제로는 z, w, b를 저장.
Forward and Backward Propagation
실제로 이러한 block을 어떻게 구성하는지 알아보자 !
Forward propagation

Backward propagation

여기서 *는 element-wise product을 의미한다.
DNN에서 역전파를 구성하려면 위 4개의 식을 알고 있어야 한다. 오른쪽은 이를 벡터화한 것이다.

요약 : forward에서 차례차례 구함 => 예측값 (y hat)을 구함 => 가중치에서 손실함수를 가중치에 대해 미분한 것을 빼면서 업데이트를 함 (backword)

사실, 머신러닝 알고리즘의 복잡성은 코드가 아닌 데이터로부터 온다.
Parameters vs Hyperparameters
하이퍼 파라미터: 러닝속도, 반복 횟수, 레이어 개수 .. 등은 파라미터인 W, b의 값을 control한다. (얼마나 많은 레이어를 가지는가. 얼마나 반복하는가 등으로 인해 직접적으로 w, b값이 바뀐다. ) 따라서 이들을 하이퍼 파라미터라고 한다. 다음 코스에서 하이퍼 파라미터에 대해 더 자세히 다룰 것이다. (mini batch size, momentum 등)
오늘날의 딥러닝은 굉장히 empirical한 process이다. (쉽게 말해, 해봐야 안다..일단 시도하고, 관찰한 뒤에, 보완해서 다시 시도)
최적의 하이퍼파라미터는 계속해서 변할 수 있다. (데이터, 컴퓨터 아키텍쳐도 계속 변화하기 때문.) / 또한, 딥러닝에는 다양한 분야가 있는데 (NLP, Speech, Vision..) 서로 적용이 가능하다.
ng 의견 : 하지만 아직 발전 분야라, 나중에 가면 어떠한 하이퍼 파라미터가 가장 좋은 갓인지에 대한 공식이 나오지않을까.
What does this have to do with the brain?
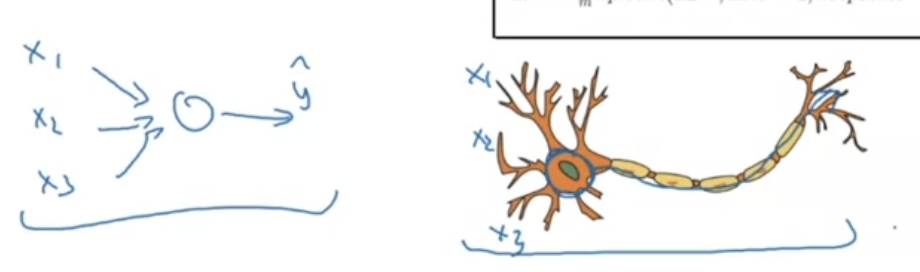
왼쪽 neural network를 오른쪽 그림인 신경망에 대하여 비유하는 경향이 많다. 왜냐하면 뉴런도 근처에 있는 다른 뉴런의 전기 신호를 받고 내부적으로 계산을 해서 다른 뉴런으로 전달하기 때문이다.
사실 아직 인간의 단일 신경망이 정확히 어떤 매커니즘으로 어떻게 일을하는지 알아내지 못했고, 뇌의 작동에서 한 뉴런이 어떠한 일을 하는지도 불명확한 상태이다. 그래서 이것은 너무 단순화한 설명이라 기피한다고 한다.
그저 우리는 X-Y 간 흥미로운 mapping 관계를 배우고 있는 것이라 보면 된다.
참고
'Deep Learning Specialization 강의 > Neural Networks and Deep Learning' 카테고리의 다른 글
| Shallow Neural Network (3주차) 정리 (0) | 2024.07.11 |
|---|---|
| Logistic Regression as a Neural Network (2주차) 정리 (0) | 2024.07.08 |
| Introduction to Deep Learning (1주차) 정리 (2) | 2024.07.03 |
